GAMES101-14&15:辐射度量学
前言
GAMES101-14:辐射度量学的意义、能量,功率与辐射强度(intensity)的定义。
GAMES101-15:辐射度量学的基本概念:辐照强度、辐射通量,BRDF,渲染方程,全局光照
辐射度量学
为什么要研究辐射度量学:Whitted-Style 光线追踪尽管可以在一些场景表现不错,但是其建立完全是基于经验值和表现的效果的,而不是实际的物理规律,因此其值不可能完全真实准确。这就是为什么我们需要辐射度量学。
要进行严谨度量,我们就要先定义单位(中文均为个人翻译,课程中没有中文名):
辐射能 Radiant Energy:辐射出的能量 Q \((J)\)。
辐射速率/功率 Radiant flux(power):单位时间内辐射/吸收/反射的能量。对于光源即“有多亮” .\(\Phi=\frac{\mathrm{d}Q}{\mathrm{d}t}\) ,单位 \(\mathrm{W(Watt)/lm(lumen)}\) > 注意:下文和图形学中说到的能量往往是指 flux 而非 energy,因为我们总是在关心眼下发生的情况(实时)而非累计的结果。
辐射强度 Radiant Intensity:一个单位立体角的功率。 \(I(\omega)=\frac{\mathrm{d}\Phi}{\mathrm{d}\omega}\),单位 \(\mathrm{cd(candela)=\frac{lm}{sr}or\frac{W}{sr}}\)。
类比弧度,立体角(Solid angel)是指 \(\Omega=\frac{S}{r^2}\),其中 S 是对应的表面积,一个球的立体角是 \(4\pi\)。将面积表示成半径 r、和 y 轴(竖直轴)的夹角 \(\theta\)、和水平面 x 轴的夹角 \(\phi\) 的组合,就有:
\[\Omega=\frac{S}{r^2}=\sin\theta\mathrm{d}\theta \mathrm{d}\phi\]
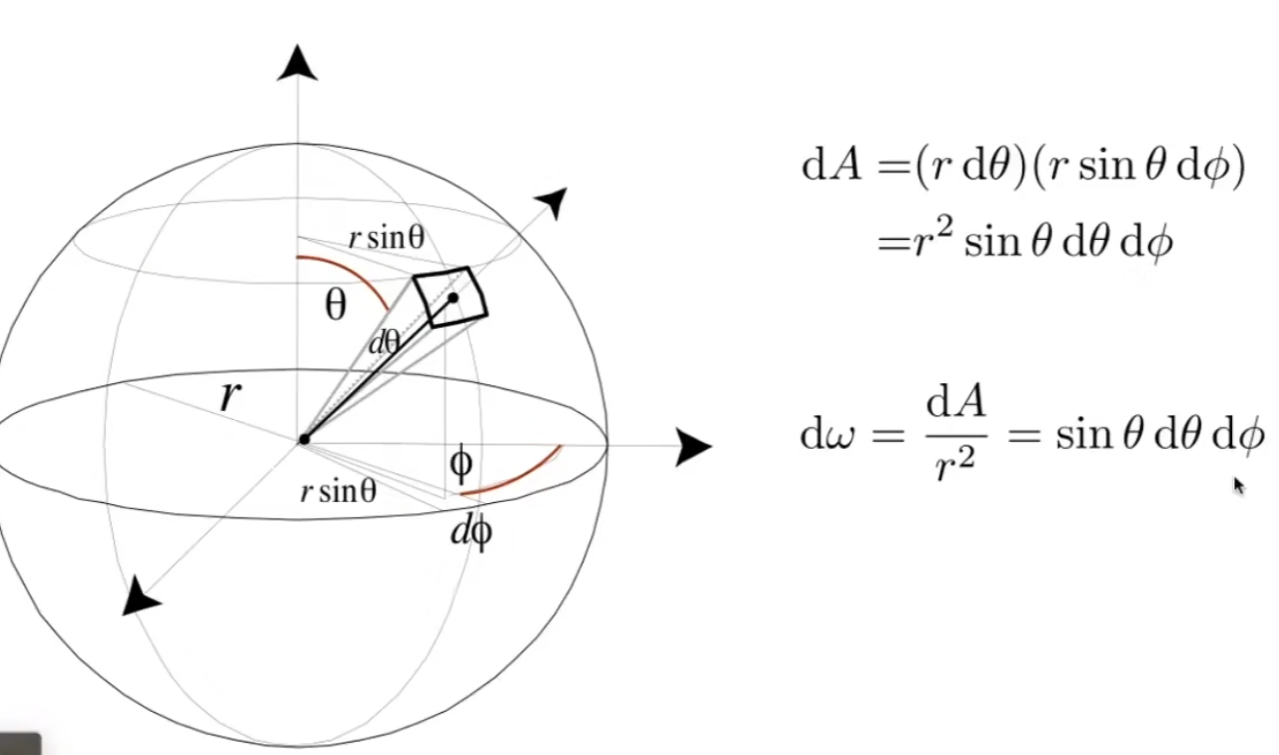
如果一个点光源均匀地向所有方向辐射光,那么 Intensity 就简单的有
\[I=\frac{\Phi}{4\pi}\]
辐照强度 Irradiance:单位面积接收到的(投影后的)能量(flux)。
\[E(x)=\frac{\mathrm{d}\Phi (x)}{\mathrm{d}S}=\frac{\Phi}{S}\cos \theta\]
单位 \(\mathrm{lux}=\frac{lm}{m^2}\)。此处要求的能量与面积是垂直的,如果不垂直则需要投影。这正是 Blinn-Phong 模型中应用的“物体接收到的光取决于与法线的余弦”(Lambert’s Cosine Law)的物理意义。
随着距离的增加,辐射强度 Intensity 不会发生改变,但是辐照度 Irradiance 会衰减。
辐射通量 Radiance:单位立体角且单位面积内的辐射能量。换句话说,通量就是单位立体角中的辐照度(理解吸收)或单位面积的辐射强度(理解发出)。通量是一个有方向的量。
\[L(p,\omega)=\frac{\mathrm{d^2}\Phi(p,\omega)}{\mathrm{d}\omega\mathrm{d}S\cos\theta}\]
单位\(nit=\frac{\mathrm{cd}}{\mathrm{m^2}}\)。 > 对来自单位面积来自所有方向的辐射积分,就有该面积的所有能量。再对面积积分,则有物体的所有接收能量。
这些概念中单位相对而言并不重要,请注意理解概念本身。
BRDF:双向反射分布函数
BRDF 的作用在于,将物体吸收的能量(Irradiance)和指定角度发出(反射)的能量(Radiance)联系了起来。对于一个极小区域 \(\mathrm{d}A\),一束从 \(\omega _i\) 入射的辐射是:
\[\mathrm{d}E(\omega_i)=L(\omega_i)\cos\theta_i\mathrm{d}\omega_i\]
物体吸收后发射(或者说物体反射)辐射到不同的方向,对于一个指定的方向 \(\omega_r\),反射的能量记为 \(\mathrm{d}L_r(\omega_r)\)。
此时,可以记 BRDF 为:
\[f_r(\omega_i\rarr \omega_r)=\frac{\mathrm{d}L_r(\omega_r)}{\mathrm{d}E_i(\omega_i)}=\frac{\mathrm{d}L_r(\omega_r)}{L(\omega_i)\cos\theta_i\mathrm{d}\omega_i}\]
BRDF 的图像描述了辐射会被反射到哪个方向,例如如果是镜面反射,那么图像就是仅在镜面反射方向有值,其他方向没有多少值。
反射方程与渲染方程
把该点的所有入射光的 BRDF 累加起来,就可以算出该点反射了多少光,即该点的反射方程:
\[L_r(p,\omega_r)=\int_{H^2}f_r(p,\omega_i\rarr \omega_r)L(p,\omega_i)\cos\theta_i\mathrm{d}\omega_i\]
添加自发光项使得公式对光源也适用:
\[ L_r(p,\omega_o)=L_e(p,\omega_o)+\int_{H^2}L_i(p,\omega_i) f_r(p,\omega_i\rarr \omega_o) (\vec{n}\cdot\vec{\omega_i}) \mathrm{d}\omega_i \]
此时方程就是渲染方程。需要指出的是涉及的向量的方向都是从 p 点指向外的,而且通过积分域的限制,我们排除了下半球内的积分,因为这个方向肯定不会对渲染起作用。(相当于 Blinn-Phong 模型中的那个 max() )。而且通过积分,我们不仅可以处理多个点光源,也可以处理面光源。
全局光照
把上面的式子简单分析一下,其实就是:反射光=自发光+入射光BRDF余弦角。其中未知量只有入射光和反射光。于是我们经过一系列的简化就可以有:
\[L=E+KL\]
其中 I 是单位矩阵,因为反射的和入射能量没有改变所以两侧 L 相等可以直接合并。
考虑到入射的 L 也可以是其他物体反射的 L,所以类似泰勒展开有
\[ L=E+KL\\ \rArr L=(I-K)^{-1}E \rArr L=E+KE+K^2E+K^3E+\dots \]
其中, E 即直接进入摄像机的光,KE 即直接打在物体表面的光,二次即一次物体反射的间接光照,三次即在物体上反射了两次才打到渲染物体上的光……依此类推。
光栅化可以较容易的处理前两项,但是很难处理后面的项。这也是为什么我们需要光线追踪。
将所有的光进行考虑得出的结果就是全局光照。下面给一些计算了不同次数反射的全局光照结果对比。
仅直接光(效果类似相机): 
一次弹射,直接光+间接光(E+KE+K^2E): 
两次弹射: 
四次弹射(效果愈发接近人眼): 
随着次数的增加,弹射对效果的影响愈发的小,也愈发的接近人眼的效果。
需要注意的是,一次和二次光照的时候,屋顶的灯光反而变黑了,这是因为这里光两次折射还没有折出灯管,因此造成了错误。
最后说了一些概率论基础,没有特别需要记的必要。
跳转
Home:GAMES101-1:课程总览与笔记导航