GAMES101-10&11：隐式几何与显式几何

发表于 2023-07-31 更新于 2024-04-21 分类于 GAMES101 Disqus：本文字数： 709

前言

GAMES101-10:隐式几何
GAMES101-11:显式几何

用三角形面并不能很好的面对所有的情形，例如：庞大的城市如何简化远景、狗身上繁复细密的毛发、轻薄半透的纱衣……

CG 中将几何分为隐式几何与显式几何。下面分别讨论。

隐式几何：不指明点的位置，但是指明点的关系。例如 $x^2+y^2+z^2=1$ 。更通用地，隐式几何指明 $f(x,y,z)=0$ 。

隐式几何很难判断有满足条件的点都有哪些，但是很容易知道指定的一个点是否满足条件（在几何面上）。

在简单的几何情况下，我们容易写出f（x），但是几何体过于复杂时，虽然也可以找到合适的函数（傅里叶？），但是我们可以采用构造实体几何（CSG）的办法：

构造实体几何：对基本的隐式几何体进行基本的布尔运算（交并补等）得到复杂的几何（参考工图作业图）。

此外对于隐式几何我们还可以用距离函数：

距离函数：对任意一个点定义与几何体的，例如在面上距离为 0，面外为正，面内为负。

通过距离函数我们可以实现两个图形相融合的效果（空间中的点同时受到两个面的距离的拉扯），例如

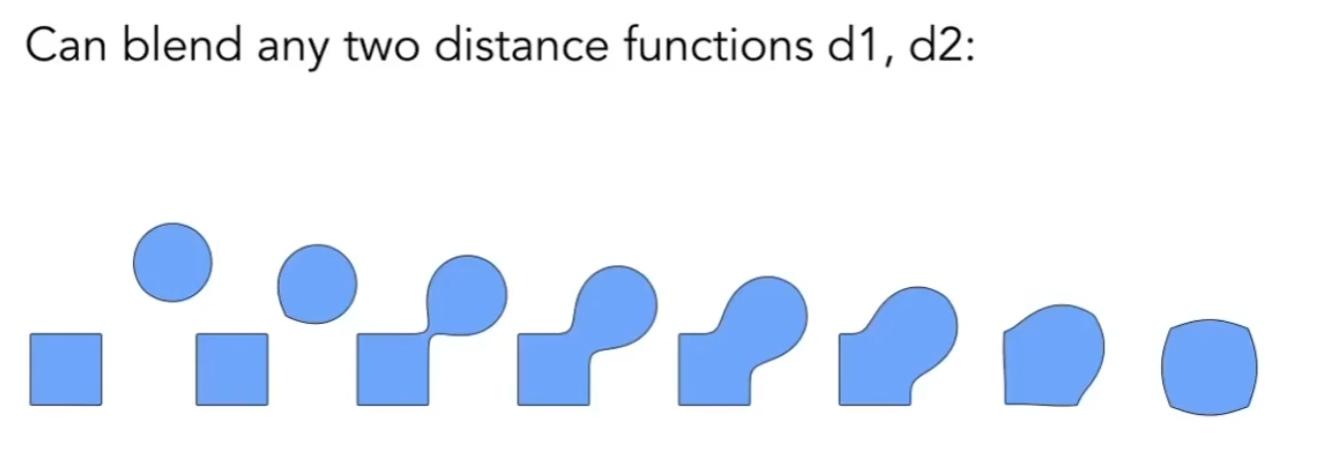
融合几何体

空间中的一个点在图形 AB 的距离分别是 a，b，那么最后距离为 a+b，最后找出 a+b = 0 的地方就是融合后的新面上的地方。

为了表示好复杂情况下的等距离点的集合，我们应用水平集这个概念表示同一个水平线的点的集合，类似等高线。

如果定义在三维，存储为纹理图，那么我们就可以找到一个有同一特征的面形成纹理。

隐式几何我们还可以很方便的表示分形图形。

显示几何的定义方法是直接给出（例如前面章节提到的三角形面）或参数映射（例如每个（u，v）都能映射到一个（x，y，z））。

相对地，显式几何难以判断点是否在几何面上。

显式几何的一些例子：