GAMES101-3:变换
前言
GAMES101-P3:基本线性变换(旋转、缩放、切变)和平移、仿射变换矩阵、齐次坐标、三维变换中的旋转问题。
对图形进行各种变换,可以相当于对其左乘对应矩阵。
基本线性变换
缩放矩阵 \(\begin{bmatrix} s_x & 0\\ 0 & s_y \end{bmatrix}\)
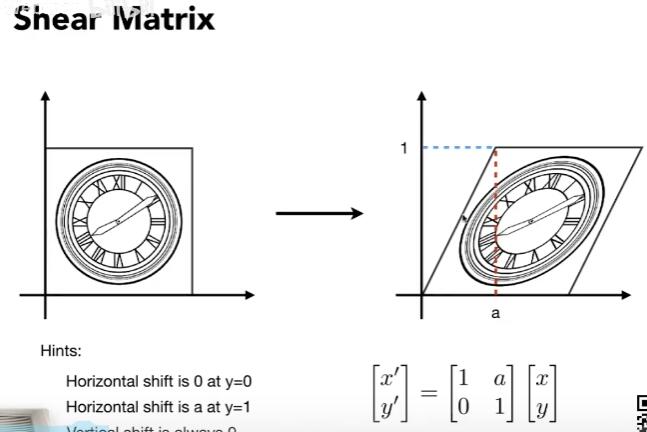
切变 (Shear) 矩阵: \(\begin{bmatrix} 1 & a\\ 0 & 1 \end{bmatrix}\)
切变的本质就是将矩形变成平行四边形。坐标不变的一条边称之为依赖轴,变换称之为方向轴。下图为一个 y 为依赖轴的例子:
旋转:旋转点通常是原点。\(\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}\)
对旋转矩阵,其反方向旋转的对应矩阵为其逆矩阵同时也是转置矩阵。
齐次坐标和仿射变换
使用 \(n+1\) 维坐标表示 \(n\) 维坐标。其中,对于点,记为 \((x,y,1)^T\),对于向量,记为 \((x,y,0)^T\)
由于平移,不能写成左乘形式进而与其余变换统一。所以我们引入齐次坐标,使得平移矩阵为 \(\begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix}\)
思考:为什么向量和点的第三维不一样?
对于向量,具有平移不变性,我们不希望其左乘平移矩阵得到的结果是新的向量,对于点的想法则相反。因此向量的最后一维应为 0 使得其不受平移矩阵影响。
进一步地,有:
- 向量 + 向量 = 向量
- 向量 + 点 = 点
- 点 - 点 = 向量
- 点 + 点 = 二者中点
- ……
可以发现向量为 0 而点为 1 的情况对于上述现象也可以解释得很好。
仿射变换
定义仿射变换:仿射变换 = 线性变换 + 平移。
使用齐次坐标可以表示仿射变换。齐次坐标等于多个线性变换矩阵、平移变换矩阵左乘后的结果。
\[M=\begin{bmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{bmatrix}\]
其中 \(a,b,c,d\) 表示旋转、缩放、切变,\(t_x,t_y\) 表示平移。
逆矩阵
对于仿射变换矩阵 M,定义逆矩阵:
\[MM^{-1} = E\]
其中 E 为单位矩阵。
M 的逆矩阵恰好对应原来仿射变换的逆变换。
特别地,对于旋转变换,其逆矩阵和转置矩阵相同,使得求其逆变换变得方便。逆矩阵等于转置矩阵的矩阵被称为正交矩阵。
矩阵不满足交换律,变换也不满足交换律。变换的顺序很重要。
绕任意点的旋转
设任意点为 P,将旋转分解为:把 P 平移回原点、旋转 α 度、平移 P 回 P 点。
于是有变换矩阵:
\[T = T(P)T(\alpha)T(-P)\]
(注意顺序是由右到左表示的)
三维变换
对于三维变换,可以简单地写出缩放和平移,重点关注旋转。
绕轴旋转
考虑简单的旋转:绕一个轴在一个平面内旋转。
\[R_x=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha & 0 \\ 0 & \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \] \[ R_y=\begin{bmatrix} \cos\alpha & 0 & \sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\alpha & 0 & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \] \[ R_z=\begin{bmatrix} \sin\alpha & \cos\alpha & 0 & 0 \\ \cos\alpha & -\sin\alpha & 0 & 0\\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
请注意 y 轴中 \(sin\alpha\) 的正负号与其他情况不同。
这是因为旋转矩阵的循环对称性。即 xyzxyz 的矩阵循环中,一个的值等于前面两个的值相乘。所以对 R_y 有 \(R_z \times R_z = R_y\) 而非相反。
绕任意轴旋转
对于任意角度的过原点轴,可以把它分解为三个轴上的角度(欧拉角)。变成三个轴的变换矩阵的乘积。
对绕任意轴 \(n\) 旋转 \(\alpha\) 角,有 Rodrigues’ Rotation Formula 如下: \[ \bold{R}(\bold{n},\alpha) = \cos(\alpha)\bold{I}+(1-\cos(\alpha))\bold{n}\bold{n^T}+\sin(\alpha)\bold{N} \] 其中 \[ \bold{N}=\begin{bmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{bmatrix} \]
其中,称 \(\bold{N}\) 为 n 的反对称矩阵,也就是向量 n 的叉积(\(\vec{n}\times\bold{\vec{a}}\) )的矩阵形式。
对于任意不过原点的旋转,把其分解为平移原点、旋转、平移回去的过程。
引入四元数是为了更好地对旋转进行插值,关于四元数,另行参考。
跳转
Home:GAMES101-1:课程总览与笔记导航
Prev:GAMES101-2:回顾线代
Next:GAMES101-4:视图和投影变换