GAMES101-4：视图和投影变换
前言
GAMES101-P4：视图变换和投影变换（正交投影、透视投影）。透视投影部分内容在原视频P5
如何拍一张照片：MVP变换
Model Transformation:摆好位置
View Transformation：找好拍照角度
Projection Transformation：拍照。
视图变换：View
思考：任何情况下进行拍照，照片都只和物体相对于相机的坐标有关。
所以建立一个新的坐标系（相机坐标系）规定
- 相机处于原点；
- 相机的向上方向是 Y （up at Y）；
- 相机看向 -Z 方向。
将坐标转换：
- 平移相机至原点
- 旋转使向上方向为 Y，旋转使相机看向的方向为 -Z。
求此处旋转矩阵，可以求坐标轴旋转为相机轴的旋转矩阵，然后转置。
投影变换：Projection
两种投影方式：
- Orthographic Projection：正交投影
- Perspective Projection：透视投影
透视投影更接近人眼成像，会有“近大远小”、“平行线相交于一点”等效果。
在如下图所示的模型中，透视事实上就是拍下了锥形视野内的 [n,f] 内的一段区间内的物体，正交则是相机处于无限远处的一个特例。
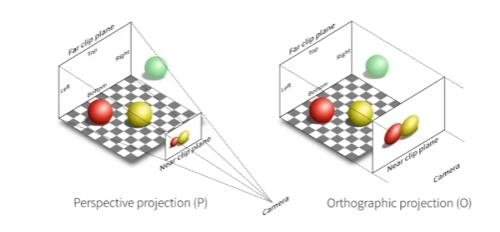
正交投影
- 构建相机坐标系
- 构建一个包含所有物体的空间立方体，描述它为 \([l,r]×[b,t]\times [f,n]\) 的一个立方体（左右下上远近）。是由远及近是由于右手坐标系且看向 -Z 方向导致远处 Z 坐标更小。
- 将结果规范化在一个 \([\pm1,\pm1, \pm1]\) 的方块内
矩阵形式：中心移至原点，再缩放 \[ M_z=\begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{b+t}{2}\\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
透视投影
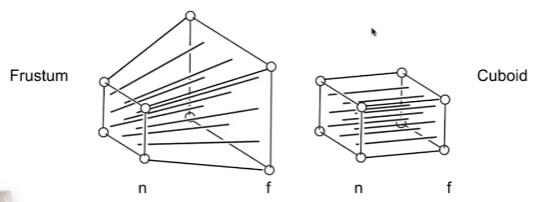
对如上图的透视，定义近平面 n 和远平面 f，有：
- 近平面保持不变，其余地方进行“挤压”使得其与近平面一样大。使上图左侧变成右侧形状。
- 进行正交投影
透视投影的变换矩阵
这里有一个需要注意的地方是，挤压以后，坐标的 Z 轴值“可能”会发生变化。对此我们规定：
- n 平面上的坐标不变
- f 平面上的坐标 Z 轴不变，且平面中点坐标不变
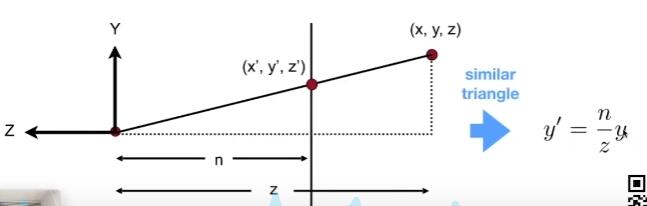
对于任意的点 \((x,y,z)\) ，对应到一个 n 平面上的点 \((x',y',z')\)。相似三角形有
\[\begin{align} y' =\frac{n}{z}y\\ x'=\frac{n}{z}x \end{align}\]
接下来求解 Z 轴的变换方程，即矩阵的第三行。
假设变换矩阵为 M，有：
\[M(x,y,z,1)^T=(\frac{n}{z}x,\frac{n}{z}y,z_1,1)^T=(nx,ny,z_2,z)^T\]
其中 \(z_1,z_2\) 未知。
\(z_1\) 的值的变换向量是 M 矩阵中的第三行，所以可以只关心第三行。又因为 Z 坐标值显然和 XY 没有关系，所以此行可以写为 \((0,0,A,B)\) 其中 A、B 未知。
n 平面上的点满足变换矩阵且 Z 坐标不变。所以 n 平面上的坐标可以写成 \((x,y,n,1)^T\) 。同时乘以坐标 n，代表的点依然不变：\((nx,ny,n^2,n)^T\)。
所以有 \((0,0,A,B)(x,y,n,1)^T=n^2\)
f 平面同样中点 \((0,0,f,1)\) 满足变换矩阵且 Z 坐标不变。于是
\[(0,0,A,B)(0,0,f,1)^T=f^2\]
于是可以联解
\[\begin{align} An+B =n^2\\ Af+B =f^2 \end{align}\] 得 \[\begin{align} A = n+f\\ B = -nf \end{align}\]
所以解出 Z 轴变换方程值， M 矩阵
\[\begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{bmatrix}\]
近平面的表示方法：可视角度
我们通常认定近、远平面的深度（z轴）是已知的，所以现在的问题是如何描述近平面：
指定近平面四个点的坐标
指定宽高比和可视角度。下图为 y 轴可视角度的表示，根据 y 轴可视角度和宽高比可以求出 x 轴的可视角度
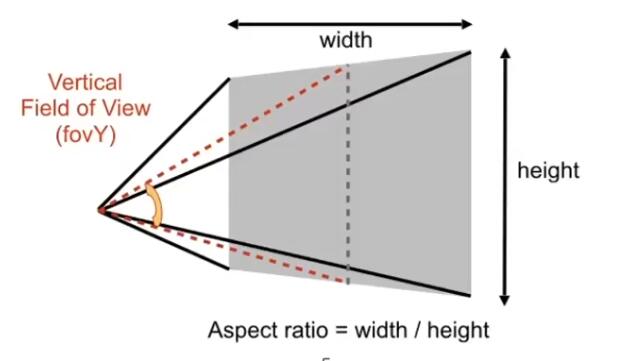
两种表示是可以互相转换的，如下：
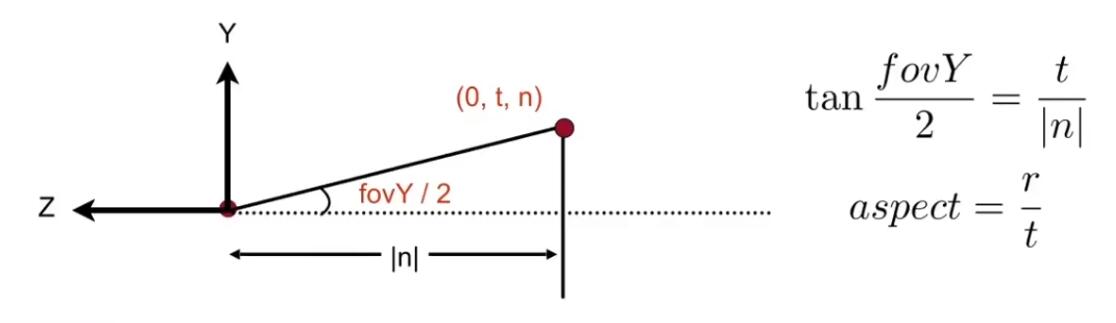
其中近平面的范围为\([\pm r,\pm t]\)，aspect 为宽高比。
跳转
Home：GAMES101-1：课程总览与笔记导航
Prev：GAMES101-3：变换
Next：GAMES101-5：(三角形的)光栅化