毕业设计（3）：RSA多小密钥指数变体的密码学分析

发表于 2024-04-20 更新于 2026-01-15 分类于毕业设计本文字数： 9k

前言

论文翻译。原名Cryptanalysis of Variants of RSA with Multiple Small Secret Exponents，INDOCRYPT 2015。

❗：由于硬盘损坏，原始翻译已遗失。现稿经由 Deepseek 由 HTML 转录而来。数学公式可能存在不准确的情况。

摘要

在本文中，我们分析了 RSA 公钥加密系统的两种变体的安全性，其中使用了多个加密和解密指数，并且这些指数共用一个模数。对于最为知名的变体 CRT-RSA，假设有 $n$ 个加密和解密指数 $(e_l, dp_l, dq_l)$，其中 $l=1,\ldots,n$，与一个共用的 CRT-RSA 模数 $N$ 一同使用。通过利用基于 Minkowski 求和的格构造，并结合几个共享一个变量的模方程，我们证明了当对所有 $l=1,\ldots,n$，有 $dp_l, dq_l < N^{\frac{2n-3}{8n+2}}$ 时，可以对 N 进行因式分解。我们进一步将这一边界提高到对所有 $l=1,\ldots,n$，$dp_l$（或 $dq_l$） $< N^{\frac{9n-14}{24n+8}}$。此外，我们的实验结果在使用多个指数时优于以前的作品，例如 Jochemsz-May (Crypto 2007)和 Herrmann-May (PKC 2010)。对于 Takagi 的 RSA 变体，假设有 $n$ 个密钥对 $(e_l, d_l)$，其中 $l=1,\ldots,n$，可用于一个共同的模数 $N = p^r q$，其中 $r \ge 2$。通过解决若干个同时的模一元线性方程，我们证明了当对所有 $l=1,\cdots,n$，$d_l < N^{ \left( \frac{r-1}{r+1} \right)^{\frac{n}{n+1}} }$ 时，可以对共同的模数 $N$ 进行因式分解。

介绍

自从 RSA 公钥方案的发明以来[16]，由于其有效的加密和解密，它已被广泛应用。为了获得高效性，一些原始 RSA 的变体被设计出来。Wiener [24]提出了一种算法，在解密阶段使用中国剩余定理来加速解密操作，通过使用满足 $e dp \equiv 1 \mod (p-1)$ 且 $e dq \equiv 1 \mod (q-1)$ 的较小指数 $dp$ 和 $dq$，其中模数为 $N = p q$，加密指数为 e。这种解密导向的 RSA 方案通常被称为 CRT-RSA。同样为了获得快速解密实现，Takagi [21]提出了另一种 RSA 的变体，其模数形式为 $N = p^r q$，其中 $r \ge 2$ 是一个整数。对于 Takagi 的变体，加密指数 $e$ 和解密指数 $d$ 满足 $e d \equiv 1 \pmod{p^{r-1}(p-1)(q-1)}$。

在 RSA 方案及其变体的许多应用中，要么选择 $d$ 较小，要么选择 $dp$ 和 $dq$ 较小以便在解密过程中进行高效的模指数运算。然而，自从 Wiener [24]展示了当 $d$ 足够小时原始 RSA 方案不安全，沿着这个方向，许多研究人员都对在小解密指数下对 RSA 模数及其变体的因式分解给予了极大关注。

RSA 及其变体的小指数攻击: 对于原始的 RSA，当 $d \le N^{0.25}$ 时，Wiener [24]证明了可以通过连分数法在多项式时间内因式分解模数 $N$。后来，Boneh 和 Durfee [2]利用了一种基于格的方法，该方法通常被称为 Coppersmith 技术 [5]，用于寻找模方程的小根，他们在几个可接受的假设下将界限提高到了 $N^{0.292}$。随后，Herrmann 和 May [6]使用了一种线性化技术简化了所涉及的格的构造，并获得了相同的界限 $N^{0.292}$。到目前为止，$N^{0.292}$ 仍然是对具有完整 $e$ 大小的原始 RSA 方案的小秘密指数攻击的最佳结果。

对于 CRT-RSA，Jochemsz 和 May [10]提出了一种针对小 $dp$ 和 $dq$ 的攻击，其中 $p$ 和 $q$ 是平衡的，加密指数 $e$ 的大小是完整的，即大约与模数 $N = p q$ 一样大。通过解一个整数方程，他们可以因式分解 $N$，前提是小的解密 CRT 指数 $dp$ 和 $dq$ 小于 $N^{0.073}$。同样，Herrmann 和 May [6]使用了一种线性化技术获得了相同的理论界限，但在实验中取得了更好的结果。

对于具有模数 $N = p^r q$ 的 Takagi 的 RSA 变体，May [13]应用了 Coppersmith 的方法证明了可以因式分解模数，前提是 $d \le N^{ \left( \frac{r-1}{r+1} \right)^2 }$。通过修改构造格中的多项式集合，Lu 等人 [12]将这个界限提高到了 $d \le N^{ \frac{r(r-1)}{(r+1)^2} }$。最近，从利用代数性质 $p^r q = N$ 的新视角出发，Sarkar [17]改进了当 $r \le 5$ 时的界限。特别是对于 $r=2$ 的最实际情况，界限从 $N^{0.222}$ 显著提高到了 $N^{0.395}$。下表列出了 RSA 及其变体的现有小解密指数攻击情况。

多个小秘密指数的 RSA:为了简化 RSA 密钥管理，人们可能会为几个密钥对 $(e_i, d_i)$ 使用单个 RSA 模数 $N$。Simmons [19]表明，如果一条消息 $m$ 发送给两个公钥指数互质的参与者，那么消息 $m$ 很容易恢复。然而，Simmons 的攻击无法因式分解 $N$。因此，Howgrave-Graham 和 Seifert [8]分析了对于一个共同的模数 $N$ 存在多个可用的加密指数 $(e_1, \cdots, e_n)$ 以及相应的小解密指数 $(d_1, \cdots, d_n)$ 的情况。根据他们的结果，对于 $l=1, \cdots, n$，当 $n$ 个解密指数满足 $d_l < N^{\delta}$ 时，可以因式分解 $N$，其中

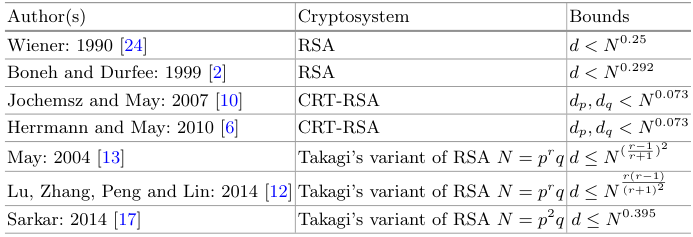
\[ \delta < \begin{cases} \frac{(2n+1)2^n - (2n+1)\binom{n}{n/2}}{(2n-1)2^n + (4n+2)\binom{n}{n/2}}, & \text{若 } n \text{ 为奇数}, \\ \frac{(2n+1)2^n - 4n\binom{n-1}{(n-1)/2}}{(2n-2)2^{2n} + 8n\binom{n-1}{(n-1)/2}}, & \text{若 } n \text{ 为偶数}. \end{cases} \] table 1

Table 1: 小秘密指数攻击 RSA 及其变体的现有研究概况。最后一列中的条件允许高效因式分解模数 $N$。

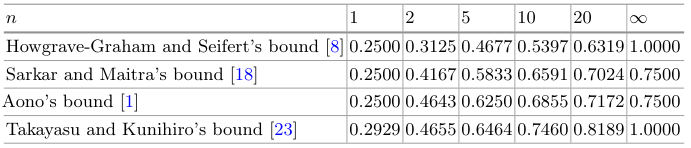
Table 2: 就解密指数数量而言，以前的理论界限的比较。

在[18]中，Sarkar 和 Maitra采用了[9]中的策略来解决一个整数方程的小根，并将界限提高到了 $\delta < \frac{3n-1}{(4n+4)}$。Aono [1]提出了一种解决多个同时的模方程的方法，这些方程共享一个未知变量。Aono 通过基于 Minkowski 求和的格构造将几个格合并成一个格，并得出当 $\delta < \frac{9n-5}{12n+4}$ 时，可以对 $N$ 进行因式分解。随后不久，Takayasu和Kunihiro [23]修改了每个格，并收集了更多有用的多项式，将界限改进到了 $1-\sqrt{\frac{2}{3n+1}}$。总之，前期工作的明确比较如表2所示。

模未知除数的同时模一元线性方程：2001年，Howgrave-Graham 首次考虑了解决一个未知除数的已知复合整数的模一元线性方程的问题，形式为

\[ f(x) = x + a \pmod{p} \]

其中 $a$ 是给定的整数，$p \simeq N^{\beta}$ 是已知 $N$ 的未知因子。根的大小受到 $|x| < N^{\delta}$ 的限制。Howgrave-Graham 证明了只要 $\delta < \beta^2$，就可以在多项式时间内求解根。

Cohn 和 Heninger [4]考虑了这个问题的一般化：

\[ \begin{cases} f(x_1) = x_1 + a_1 \pmod{p}, \\ f(x_2) = x_2 + a_2 \pmod{p}, \\ \quad \cdot \cdot \cdot \\ f(x_n) = x_n + a_n \pmod{p}. \end{cases} \]

在上述的同时模一元线性方程中，$a_1,\cdots,a_n$ 是给定的整数，而 $p \simeq N^{\beta}$ 是 $N$ 的一个未知因子。根据他们的结果，如果满足以下条件，就可以对 N 进行因式分解：

\[ \frac{\gamma_1 + \cdot\cdot\cdot + \gamma_n}{n} < \beta^{\frac{n+1}{n}} \,\text{ 且 } \beta \gg \frac{1}{\log N} \]

其中 $|x_1| < N^{\gamma_1},\ldots,|x_n| < N^{\gamma_n}$。然后，通过考虑未知变量的大小并收集更多有用的多项式来构造格，Takayasu 和 Kunihiro [22]进一步将界限改进为

\[ \sqrt[n]{\gamma_1 \cdots \gamma_n} < \beta^{\frac{n+1}{n}} \,\text{且}\ \beta \gg \frac{1}{\sqrt{\log N}} \]

我们的贡献：在本文中，我们分别对 CRT-RSA 和 Takagi 的 RSA 变体进行了多个小解密指数的分析。对于 CRT-RSA，$(e_1,\cdots,e_n)$ 是 $n$ 个加密指数，而 $(dp_1,dq_1),\cdots,(dp_n,dq_n)$ 是对一个共同的 CRT-RSA 模数 $N$ 的相应解密指数，其中 $e_1,\cdots,e_n$ 与 $N$ 位长相同。基于 Aono [1]提出的基于 Minkowski 求和的格构造，我们结合了几个共享一个公共变量的模方程，并得出了结论，当对所有 $l = 1, \ldots , n$,其中解密指数的数量为 $n$ 时，

\[ dp_l,dq_l < N^{\frac{2n-3}{8n+2}} \]

为了利用基于 Minkowski 求和的格构造来合并方程，这些方程应该共享一个公共变量。因此，我们修改了[10]中考虑的每个方程，当只有一对加密和解密指数时，它们导致了一个更差的界限。

然而，注意到模方程

\[ kp_l(p-1)+1 \equiv 0 \pmod{e_l} \]

对于 $l=1,\ldots,n$，共享一个公共根 $p$。然后，我们可以通过基于 Minkowski 求和的格构造直接组合这些 $n$ 个方程，而且引入了一个新变量 $q$ 来最小化组合格的行列式。我们可以得到一个改进的界限，即当对所有 $l = 1, \ldots , n$ 时，$dp_l < N^{\frac{9n-14}{24n+8}}$。

需要注意的是，为了组合这些方程，我们修改了[10]中考虑的每个方程。当有 $n=2$ 个解密指数时，我们的界限是 $N^{0.071}$，小于[10]中的界限 $N^{0.073}$。因此，我们只在存 $n \ge 3$ 对共用一个共同的 CRT-RSA 模数加密和解密指数时，在理论上改进了之前的界限，并在渐近情况下获得了 $N^{0.375}$。然而，令人欣慰的是，我们成功地通过实践在 $dp_l < N^{0.035}$ 的情况下使用了3对指数因式分解 $N$，并且原始界限是[10]中的 $N^{0.015}$ 和[6]中的 $N^{0.029}$。

这些界限的明确描述如图1所示。

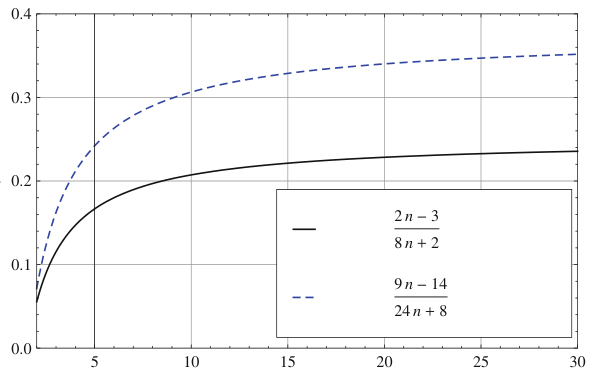
Fig. 1. CRT-RSA 的秘密指数可恢复的范围。实线表示 $dp_l$ 和 $dq_l$ 与 $n$ 的关系范围，虚线表示 $dp_l$ 与 $n$ 的关系范围。

对于 Takagi 的 RSA 变体，假设存在 $n$ 个加密和解密指数 $(e_l,d_l)$，其中 $l = 1, \ldots , n$ 共用一个模数 $N = p^r q$，这意味着存在 $l$ 个同时的模一元线性方程。到目前为止，这种模方程是[4,22]中考虑的内容。通过应用它们的结果，我们得出结论，当对所有 $l = 1, \ldots , n$ 时，$d_l \le N^{\delta}$ 时，可以对模数进行因式分解，其中

\[ \delta < \left( \frac{r-1}{r+1} \right)^{\frac{n+1}{n}} \]

本文的其余部分安排如下。第2节是关于格和 CRT-RSA 变体的一些初步知识。在第3节中，我们分析了具有多个小解密指数的 CRT-RSA。第4节介绍了对具有多个小解密指数的 Takagi 的变体 RSA 的分析。最后，第5节是结论。

2. 预备知识

让 $w_1,w_2,\cdots,w_k$ 为 $n$ 维空间 $\mathbb{R}^n$ 中的 $k$ 个线性无关向量。由 $w_1,\cdots,w_k$ 张成的格 $L$ 是所有 $w_1,\cdots,w_k$ 的整数线性组合 $c_1 w_1 + \cdots + c_k w_k$ 的集合，其中 $c_1,\ldots,c_k \in \mathbb{Z}$。 $k$ 维格 $L$ 是 $\mathbb{R}^n$ 中的离散加法子群。向量 $w_1,\cdots,w_k$ 的集合称为格 $L$ 的一个基。格基不是唯一的，可以通过乘以行列式为 $\pm 1$ 的任意矩阵获得另一个基，这意味着任何维数大于 $1$ 的格都有无穷多个基。因此，如何找到具有良好性质的格基一直是一个重要问题。

Lenstra 等人[11]引入了著名的 $L^3$ 格基约简算法，该算法可以在多项式时间内输出相对较短且几乎正交的格基。该算法不是寻找格中最短的向量，而是找到具有以下有用性质的 $L^3$ 约简基。

引理1（$L^3$，[11]）。 设 $L$ 是维度为 $k$ 的格。将 $L^3$ 算法应用于 $L$，输出的约简基向量 $v_1,\ldots,v_k$ 满足以下条件

\[ \| v_i \| \le 2^{\frac{k(k-i)}{4(k+1-i)}} \cdot \det(L)^{\frac{1}{k+1-i}} \]

，对于任意 $1 \le i \le k$。

Coppersmith [5]应用 $L^3$ 格基约简算法来寻找整数方程和模方程的小解。后来，Jochemsz 和 May [9]扩展了这一技术，并给出了找到多元多项式的根的一般结果。

对于给定的多项式 $g(x_1,\cdots,x_k)=\sum_{(i_1,\ldots,i_k)} a_{i_1,\ldots,i_k} x_1^{i_1} \cdots x_k^{i_k}$，我们定义 $g$ 的范数为

\[ \| g(x_1,\ldots,x_k) \| = \left( \sum_{(i_1,\ldots,i_k)} a_{i_1,\ldots,i_k}^2 \right)^{\frac{1}{2}} \]

Howgrave-Graham [7]的以下引理给出了将模方程转换为整数方程的一个充分条件。

引理2（Howgrave-Graham，[7]）。 设 $g(x_1,\ldots,x_k) \in \mathbb{Z}[x_1,\ldots,x_k]$ 是一个最多有 $w$ 个单项式的整数多项式。假设

\[ g(y_1,\cdots,y_k) \equiv 0 \pmod{p^m} \text{ 对于成立 } |y_1| \le X_1,\cdots,|y_k| \le X_k \text{ 并且 } \| g(x_1 X_1,\ldots,x_k X_k) \| < \frac{p^m}{\sqrt{w}} \]

那么在整数域上 $g(y_1,\ldots,y_k)=0$ 成立。

假设我们有 $w(>k)$ 个多项式 $b_1,\ldots,b_w$，它们是关于变量 $x_1,\ldots,x_k$ 的，满足 $b_1(y_1,\ldots,y_k) = \cdots = b_w(y_1,\ldots,y_k) = 0 \pmod{p^m}$，其中 $|y_1| \le X_1,\ldots,|y_k| \le X_k$。现在我们构造一个由 $b_1(x_1 X_1,\ldots,x_k X_k),\ldots,b_w(x_1 X_1,\ldots,x_k X_k)$ 的系数向量构成的格 $L$。经过格约简后，我们得到 $k$ 个多项式 $v_1(x_1,\ldots,x_k),\ldots,v_k(x_1,\ldots,x_k)$，满足

\[ v_1(y_1,\ldots,y_k) = \cdots = v_k(y_1,\ldots,y_k) = 0 \pmod{p^m} \]

它们对应于约简基的前 $k$ 个向量。同时由 $L^3$ 算法的性质，我们有

\[ \| v_1(x_1 X_1,\ldots,x_k X_k) \| \le \cdots \le \| v_k(x_1 X_1,\ldots,x_k X_k) \| \le 2^{\frac{w(w-1)}{4(w+1-k)}} \det(L)^{\frac{1}{w+1-k}}. \]

因此根据引理2，如果

\[ 2^{\frac{w(w-1)}{4(w+1-k)}} \cdot \det(L)^{\frac{1}{w+1-k}} < \frac{p^m}{\sqrt{w}} \]

那么我们有 $v_1(y_1,\ldots,y_k) = \cdots = v_k(y_1,\ldots,y_k) = 0$。接下来我们想要从 $v_1,\ldots,v_k$ 中找到 $y_1,\ldots,y_k$。

一旦我们从 $L^3$ 格基约简算法得到了几个整数多项式方程，我们就可以通过计算多项式的结式(resultant)或Gröbner基来解出整数根，这基于以下的启发式假设。在实际实验中，以下的启发式假设通常成立。

假设1： 我们基于格的构造产生了代数无关的多项式。这些多项式的公共根可以通过计算结式或找到Gröbner基等技术来高效地计算。

与其他格约简工作类似[1,9,10,23]，虽然我们提供了实验结果支持我们的攻击，但我们也想指出理论结果是渐近的，因为我们在攻击计算中在某些情况下忽略了常数。

基于 Minkowski 求和的格构造: 在[1]中，Aono 提出了一种用于同时模方程 Coppersmith 技术的格构造方法。为了阐明这一点，让我们通过一个例子来说明。假设有两个模方程 $f_1 \equiv 0 \pmod{W_1}$ 和 $f_2 \equiv 0 \pmod{W_2}$。基于 Coppersmith 的技术，为了解 $f_1$ 的解，我们首先选择一些多项式 $g_1,\ldots,g_n$，它们在模 $W_1^m$ 下具有相同的解。类似地，我们构造多项式 $g_1',\ldots,g_n'$，它们在模 $W_2^m$ 下具有相同的解。显然，任何多项式 $g_i g_j'$，其中 $1 \le i,j \le n$，都具有模 $W_1^m W_2^m$ 下的所需解。然后我们排列这些多项式，并构造一个新的格，其中的多项式在 $W_1^m W_2^m$ 下具有所需的解。通过整数线性组合，其中一些具有相同首项的多项式可以写成 $\sum_{i,j} a_{i,j} g_i g_j'$。为了保持格的行列式较小，整数 $a_{i,j}$ 会适当地选择。这个格称为由多项式 $g_1,\ldots,g_n$ 构造的格和由多项式 $g_1',\ldots,g_n'$ 构造的格的合并格。 Aono证明了如果每个格都有三角形的基矩阵，那么合并的格将是三角形的。上述结论可以推广到任意数量的模方程。

CRT-RSA，即中国剩余定理 RSA，是 RSA 公钥加密系统的一种变体。自从 RSA 公钥加密系统的发明以来，由于其简洁有效的加密和解密方式，该公钥方案已被广泛应用。Wiener [24] 提出在解密阶段使用中国剩余定理。这个方案通常被称为 CRT-RSA。基于 Sun 和 Wu 的工作 [20]，这个变体的一个版本可以描述如下：

在 CRT-RSA 的密钥生成算法中描述了这样一种情况：可能存在多个有效的加密和解密指数对应于相同的 CRT-RSA 模 $N = pq$，也就是说，当我们完成第一步选择一对 $(p,q)$ 时，在剩下的步骤中我们生成了几个不同的 $dp$ 和 $dq$。接下来，我们分析多个加密和解密指数共享相同 CRT-RSA 模数的弱点。

3 CRT-RSA的多重加密和解密指数攻击

在这一部分，沿用[1,8,18,23]的思路，我们给出了以下定理，用于描述当多个加密和解密指数用于一个公共的 CRT-RSA 模时的情况。通过将我们的结果与 Jochemsz 和 May 的结果[10]进行比较，我们改进了在一个公共的 CRT-RSA 模中存在 $3$ 个或更多对加密和解密指数时的界限。我们还将实验结果从[10]的 $N^{0.015}$ 和[6]的 $N^{0.029}$ 改进到了在3对指数时的 $N^{0.035}$。

定理1. 设 $(e_1,e_2,\ldots,e_n)$ 是 $n$ 个带有共同模 $N=pq$ 的 CRT-RSA 加密指数，其中 $n \ge 3$ 且 $e_1,e_2,\ldots,e_n$ 的位长度大致与 $N$ 相同。考虑到 $dp_i, dq_i \le N^{\delta}$（$i=1,2,\ldots,n$）为相应的解密指数。然后根据假设1，在

\[ \delta < \frac{2n-3}{8n+2} \]

时，可以在多项式时间内分解 $N$。

证明. 对于一对密钥 $(e_l, dp_l, dq_l)$，我们有

\[ \begin{aligned} e_l dp_l - 1 & \equiv kp_l (p-1) \\ e_l dq_l - 1 & \equiv kq_l (q-1) \end{aligned} \]

其中 $kp_l$ 和 $kq_l$ 是一些整数。

此外，通过将这两个方程相乘，我们有

\[ e_l^2 dp_l dq_l - e_l (dp_l + dq_l) + 1 = kp_l kq_l (N - s) \]

其中 $s = p + q - 1$。

那么 $(kp_l kq_l, s, dp_l + dq_l)$ 是

\[ f_l(x_l, y, z_l) = x_l(N - y) + e_l z_l - 1 \pmod{e_l^2} \]

的一个解。

此外，考虑 $n$ 个模多项式

\[\begin{equation} f_l(x_l, y, z_l) = x_l(N - y) + e_l z_l - 1 \pmod{e_l^2} \end{equation}\]

其中 $l=1,\ldots,n$。

这些多项式有一个公共的根 $(x_1,\ldots,x_n, y, z_1,\ldots,z_n) = (kp_1 kq_1, \ldots, kp_n kq_n, s, dp_1 + dq_1, \ldots, dp_n + dq_n)$，其系数的值可以大致限定为 $kp_l kq_l \simeq X_l = N^{1+2\delta}$, $s \simeq Y = N^{1/2}$，和 $dp_l + dq_l \simeq N^{\delta} = Z$，其中 $l=1,\ldots,n$。

为了解决模多项式 $f_l(x_l, y, z_l)=0 \pmod{e_l^2}$ 的所需解，其中 $l=1,\ldots,n$，基于 Aono 的思想[1]，我们首先选择了以下一组多项式来解决每个单独的方程。

\[ S_l = \left\{ x_l^{i_l} z_l^{j_l} f_l^{k_l}(x_l, y, z_l) (e_l^2)^{m-k_l} \mid 0 \le k_l \le m, 0 \le i_l \le m - k_l, 0 \le j_l \le m - i_l - k_l \right\} \]

其中 $l=1,\ldots,n$ ，并且 $m$ 是正整数。

每次(1)中对应方程的选择都会生成一个三角形基矩阵。同样地，对于每个 $l=1,2,\ldots,n$，我们可以分别构造一个三角形矩阵。基于 Minkowski 基于格构造的求和技术，这 $n$ 个的格与 $n$ 个三角形矩阵对应，它们可以共同组合成一个新的格 $L'$，其基矩阵由和有相同根的多项式是模 $(e_1^2,\ldots,e_n^2)^m$ 的解。由于每个基矩阵都是三角形的，组合的格也是三角形的。组合的基矩阵的对角线条目为

\[ X_1^{i_1} \cdots X_n^{i_n} Y^{k} Z_1^{j_1} \cdots Z_n^{j_n} (e_1^2)^{m - \min(i_1,k)} \cdots (e_n^2)^{m - \min(i_n,k)} \]

其中

\[ \begin{align*} &0 \leq i_1, \ldots , i_n \leq m, \\ &0 \leq k \leq i_1 + i_2 + \cdots + i_n, \\ &0 \leq j_1 \leq i_1, \ldots , 0 \leq j_n \leq i_n。 \end{align*} \]

然后，格的行列式可以计算如下，

\[ \begin{align*} \det(L') &= \prod_{i_1=0}^{m} \cdots \prod_{i_n=0}^{m} \prod_{k=0}^{i_1+\cdots+i_n} \prod_{j_1=0}^{m-i_1} \cdots \prod_{j_n=0}^{m-i_n} \left( X_1^{i_1} \cdots X_n^{i_n} Y^{k} Z_1^{j_1} \cdots Z_n^{j_n} (e^2_1)^{m-\min(i_1,k)} \cdots (e_n^2)^{m-\min(i_n,k)} \right) \\ &= X_1^{S_{x_1}} \cdots X_n^{S_{x_n}} Y^{S_y} Z_1^{S_{z_1}} \cdots Z_n^{S_{z_n}} (e_1^2)^{S_{e_1}} \cdots (e_n^2)^{S_{e_n}} \end{align*} \]

其中 $$

\[\begin{align*} S_{x_1} + S_{x_2} + \cdots + S_{x_n} &= \left( \frac{n^2}{18} + \frac{n}{36} \right) \frac{m^{2n+2}}{2^{n-1}} + o(m^{2n+2})\\ S_y &= \left( \frac{n^2}{36} + \frac{n}{72} \right) \frac{m^{2n+2}}{2^{n-1}} + o(m^{2n+2})\\ S_{z_1} + S_{z_2} + \cdots + S_{z_n} &= \left( \frac{n^2}{18} - \frac{n}{72} \right) \frac{m^{2n+2}}{2^{n-1}} + o(m^{2n+2})\\ S_{e_1} + S_{e_2} + \cdots + S_{e_n} &= \left( \frac{n^2}{9} - \frac{n}{72} \right) \frac{m^{2n+2}}{2^{n-1}} + o(m^{2n+2}) \end{align*}\] $$ 另一方面，维数为

\[ \dim(L') = \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{k=0}^{i_1+\cdots+i_n} \sum_{j_1=0}^{m-i_1} \cdots \sum_{j_n=0}^{m-i_n} 1 = \frac{n}{6 \cdot 2^{n-1}} m^{2n+1} + o(m^{2n+1}) \]

通过引用引理1和引理2，我们可以得到整数方程，当 \[ \begin{equation} \det(\mathcal{L}') ^ \frac{1}{\dim(\mathcal{L}')} < (e^2_1\cdots e^2_n)^m \end{equation} \]

忽略 $m$ 的低阶项并将 $X_l = N^{1+2\delta}$，$Y = N^{\frac{1}{2}}$，$Z_l = N^{\delta}$，和 $e^2_l \simeq N^2$ 代入上述不等式(2)中对于 $l=1,\ldots,n$，必要条件可以写作

\[ (1+2\delta)\left( \frac{n^2}{18} + \frac{n}{36} \right) + \frac{1}{2}\left( \frac{n^2}{36} + \frac{n}{72} \right) + \delta\left( \frac{n^2}{18} - \frac{n}{72} \right) + 2\left( \frac{n^2}{9} + \frac{n}{72} \right) \le \frac{n^2}{3} \]

即，

\[ \delta < \frac{2n-3}{8n+2} \]

然后我们得到了 $2n+1$ 个多项式，它们共享根 $(x_1,\ldots,x_n, y, z_1,\ldots,z_n)$。根据假设1，我们可以从这些多项式中找到 $x_1,\ldots,x_n, y, z_1,\ldots,z_n$。这证明了定理1的证明。

此外，除了通过 Minkowski 求和格构造来组合多项式 $e_l dp_l = kp_l (p-1) + 1$，对于 $l=1,\ldots,n$，我们还引入了一个附加变量 $q$ 来减小我们格的行列式，最终改进了定理1的界限。

更具体地说，我们首先通过利用 Minkowski 求和格构造来组合多项式 $f_l(x_l, y) = x_l(y-1) + 1 \pmod{e_l}$，对于 $l=1,\ldots,n$。然后，基于观察到格中出现的单项式，我们发现变量 $y$ 的所需根 $p$ 是模数 $N$ 的一个因子。因此，为了减小我们构造的格的行列式，我们可以引入一个对应 $q$ 的新变量 $z$。由于 $pq=N$，我们可以用 $N$ 替换 $yz$，然后通过乘以 $N$ 模 $e_1 \cdots e_n$ 的倒数。总之，我们可以得到以下定理。

定理2. 设 $(e_1,e_2,\ldots,e_n)$ 为 $n$ 个 CRT-RSA 加密指数，共用模 $N = pq$，其中 $n \ge 2$，且 $e_1,e_2,\ldots,e_n$ 的位数与 $N$ 大致相同。考虑到对应的解密指数为 $dp_l$、$dq_l$（$l=1,2,\ldots,n$）。假设对于 $l=1,2,\ldots,n$，有 $dp_l < N^{\delta}$，那么在假设1下，当

\[ \delta < \frac{9n-14}{24n+8} \]

时，可以在多项式时间内分解 $N$。

证明. 对于每对密钥 $(e_l, dp_l, dq_l)$，我们有

\[ e_l dp_l = kp_l (p-1) + 1 \]

其中 $kp_l$ 是整数。因此，$(kp_l, p)$ 是方程

\[ f_l(x_l, y) = x_l(y-1) + 1 \pmod{e_l} \]

的解。考虑 $n$ 个模多项式

\[ f_l(x_l, y) = x_l(y-1) + 1 \pmod{e_l} \]

其中 $l=1,\ldots,n$。

显然，这些多项式有共同的根 $(x_1,\ldots,x_n, y) = (kp_1, \ldots, kp_n, p)$，其系数的大小可以粗略确定为 $kp_l \simeq X_l = N^{\frac{1}{2}+\delta}$（对 $l=1,\ldots,n$）和 $p \simeq Y = N^{\frac{1}{2}}$。

为了求解所需解，我们首先选择了以下一组多项式来解决每个单一的模方程，

\[ S_l = \left\{ x_l^{i_l} f_l^{k_l}(x_l, y) (e_l)^{m-k_l} \mid 0 \le k_l \le m, 0 \le i_l \le m - k_l \right\} \]

其中 $l=1,\ldots,n$，$m$ 是正整数。

每个选择都生成一个三角基矩阵。然后，对于 $l=1,\ldots,n$，我们分别构造一个三角矩阵。我们用与模方程的解的根相同的多项式构造了基础矩阵，模 $(e_1 \cdots e_n)^m$。通过将这些基于 Minkowski 和的格构造的 $n$ 个格子结合起来，得到的与组合格 $\mathcal{L}'_1$ 相对应的对角线条目为

\[ X_1^{i_1} \cdots X_n^{i_n} Y^{k} (e_1^2)^{m - \min(i_1,k)} \cdots e_n^{m - \min(i_n,k)} \]

其中 $0 \le i_1, \cdots, i_n \le m$，$0 \le k \le i_1 + i_2 + \cdots + i_n$。

此外，注意到所需的小解包含质因数 $p$，这是模 $N = pq$ 的因子。然后，我们引入一个新变量 $z$ 作为另一个质因数 $q$，并将与 $\mathcal{L}'_1$ 中每个行向量对应的多项式乘以某个待优化的 $s$ 的幂 $z^s$。然后，我们用 $N$ 替换每个单项式 $yz$ 的出现，因为 $N = pq$。因此，与未更改的多项式相比，每个单项式 $x_1^{i_1} \cdots x_n^{i_n} y^k z^s$ 且 $k \ge s$，其系数 $a_{i_1,\cdot\cdot\cdot,i_n,k}$ 被转换为单项式 $x_1^{i_1} \cdots x_n^{i_n} y^{k-s}$ 且系数 $a_{i_1,\cdot\cdot\cdot,i_n,k} N^s$。类似地，当 $k < s$ 时，系数 $a_{i_1,\cdot\cdot\cdot,i_n,k}$ 的单项式 $x_1^{i_1} \cdots x_n^{i_n} y^k z^s$ 且 $k \ge s$ 被转换为单项式 $x_1^{i_1} \cdots x_n^{i_n} z^{s-k}$ 其系数为 $a_{i_1,\cdot\cdot\cdot,i_n,k} N^k$。

设 $Z = N^{\frac{1}{2}}$ 为未知变量 $z$ 的上界。为了使格的行列式尽可能小，我们尝试消除对角线条目中 $N^s$ 和 $N^k$ 的因子。由于 $(N, e_1 \cdots e_n) = 1$，我们只需要将相应的多项式与 $N^s$ 或 $N^k$ 模 $(e_1 \cdots e_n)^m$ 的倒数相乘。然后，格的行列式可以计算如下，

\[ \det(L_1') = X_1^{S_{x_1}} \cdots X_n^{S_{x_n}} Y^{S_y} Z^{S_z} e_1^{S_{e_1}} \cdots e_n^{S_{e_n}} \]

其中

\[ \begin{align*} S_{x_1} + S_{x_2} + \cdots + S_{x_n} &= \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{k=0}^{i_1+\cdots+i_n} (i_1 + \cdots + i_n), \\ S_y &= \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{k=s}^{i_1+\cdots+i_n} (k - s), \\ S_z &= \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{k=0}^{s-1} (s - k), \\ S_{e_1} + S_{e_2} + \cdots + S_{e_n} &= \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{k=0}^{i_1+\cdots+i_n} (nm - \min(i_1,k) - \cdots - \min(i_n,k)) \end{align*} \]

由于下式对于任意 $0 \le a,b \le n$ 成立

\[ \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} i_a i_b = \begin{cases} \frac{1}{3} m^{n+2} + o(m^{n+2}), & (a = b), \\ \frac{1}{4} m^{n+2} + o(m^{n+2}), & (a \ne b), \end{cases} \]

我们有 \[ \begin{align*} S_{x_1} + S_{x_2} + \cdots + S_{x_n} &= \left( \frac{n^2}{4} + \frac{n}{12} \right) m^{n+2} + o(m^{n+2}), \\ S_y &= \left( \frac{\sigma^2 n^2}{2} - \frac{\sigma n^2}{2} + \frac{n^2}{8} + \frac{n}{24} \right) m^{n+2} + o(m^{n+2}), \\ S_z &= \left( \frac{\sigma^2 n^2}{2} \right) m^{n+2} + o(m^{n+2}), \\ S_{e_1} + S_{e_2} + \cdots + S_{e_n} &= \left( \frac{n^2}{4} + \frac{n}{12} \right) m^{n+2} + o(m^{n+2}) \end{align*} \] 其中 $s = \sigma n m$ 且 $0 \le \sigma < 1$。

另一方面，维数为

\[ \dim(L') = \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{k=0}^{i_1+\cdots+i_n} \sum_{j_1=0}^{m-i_1} \cdots \sum_{j_n=0}^{m-i_n} 1 = \frac{n}{6 \cdot 2^{n-1}} m^{2n+1} + o(m^{2n+1}) \]

计算细节请参考附录。

通过引用引理1和引理2，我们可以得到整数方程，当 \[ \begin{equation} \det(\mathcal{L}') ^{\frac{1}{\dim(\mathcal{L}')}} < (e_1 \cdots e_n)^m \end{equation} \] 忽略 $m$ 的低阶项并将 $X_l = N^{1+2\delta}$，$Y = N^{\frac{1}{2}}$，$Z = N^{\frac{1}{2}}$，和 $e_l \simeq N$ 代入上述不等式(3)中对于 $l=1,\ldots,n$，必要条件可以写作

\[ (1+\delta)\left( \frac{n^2}{4} + \frac{n}{12} \right) + \frac{1}{2}\left( \frac{\sigma^2 n^2}{2} - \frac{\sigma n^2}{2} + \frac{n^2}{8} + \frac{n}{24} \right) + \frac{1}{2}\left( \frac{\sigma^2 n^2}{2} \right) + \left( \frac{n^2}{4} + \frac{n}{12} \right) \le \frac{n^2}{2} \]

通过选择 $\sigma = \frac{1}{4}$，我们最终得到 $\delta$ 的边界

\[ \delta < \frac{9n-14}{24n+8} \]

然后在假设 1 下，可以在多项式时间内对 $N$ 进行因式分解。至此结束定理2的证明。

我们的结果优于文献中先前的工作的原因基于以下两点观察。首先，我们可以利用 Minkowski 和格构造将 $n$ 个多项式组合起来。其次，从 $N = pq$ 的知识出发，我们可以通过引入某些因子 $z^s$ 到每个多项式中来优化格的行列式，其中 $z$ 是对应于 $q$ 的新变量，$s$ 是将在计算过程中会被优化的整数。

实验结果

需要注意的是，在定理2的计算中，我们假设 $m$ 趋向于无穷大。因此，我们的结果是一个渐近界限，因为我们忽略了 $m$ 的低阶项。如果 $m$ 和 $n$ 是固定的，满足条件(3)的最大 $\delta$ 可以很容易地计算得出。在表3中，对于每个固定的 $m$ 和 $n$，我们列出了满足式(3)的最大 $\delta$ 以及格的维数。列中限制值表示渐近界限。

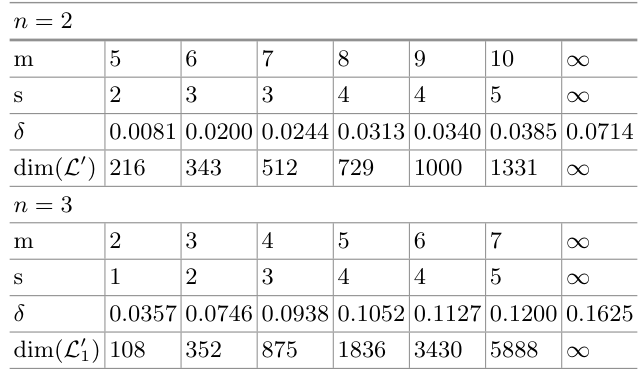
表3. 固定 $m$ 时小 $\delta$ 的理论界限和格的维数。

我们在一台配备 Intel® Core™ Duo CPU（2.53 GHz，1.9 GB RAM， Windows 7）的个人电脑上，使用 Magma 2.11计算机代数系统[3]实现了实验程序，并进行了 $L^3$ 算法[14]。实验结果如表4所示。

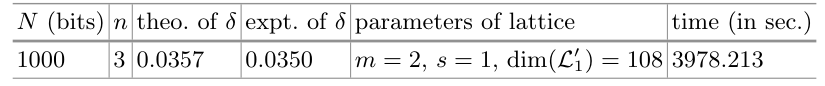
表4. 实验结果。

在实验中，我们成功地在实践中分解了共同模 $N$，当存在三个解密指数且它们都小于 $N^{0.035}$ 时。对于这个给定的问题，Jochemsz 和 May成功地分解了具有一个小解密指数的 $N$，其界限为 $N^{0.015}$，后来通过利用 Herrmann 和 May引入的未展开线性化技术，该界限已经提高到了 $N^{0.029}$。换句话说，我们通过使用更多具有共同模的解密指数，改进了理论和实验界限。

需要注意的是，在实验中，我们总是找到许多多项式方程在整数域上共享所需的解。此外，我们还有另一个方程 $yz = N$。然后通过计算这些多项式的 Gröbner 基础，我们可以在不到两个小时内成功解出所需的解。

在我们进行的所有验证我们提出的攻击的实验中，我们确实通过使用 Gröbner 基础技术成功地收集了根，并且没有实验结果与假设1相矛盾。然而，另一方面，证明或证实其有效性似乎非常困难。

4. 多重加密和解密指数攻击：Takagi变种RSA

定理3. 设 $(e_1, e_2, \dots, e_n)$ 为 Takagi 变种 RSA 的 $n$ 个加密指数，共用模 $N = p^r q$。考虑到 $d_1, d_2, \cdots, d_n$ 是相应的解密指数。那么在假设1下，当 \[ \delta < \frac{(r - 1)}{(r + 1)} ^{ \frac{n}{n + 1}} \] 时，可以在多项式时间内分解 $N$，其中 $d_l \leq N^\delta$，对于 $l = 1, \dots, n$。

证明. 对于一个模 $N = p^r q$，存在 $n$ 个加密和解密指数 $(e_l, d_l)$，因此，我们有 \[ \begin{aligned} e_1 d_1 &= k_1 p^{r-1}(p - 1)(q - 1) + 1, \\ e_2 d_2 &= k_2 p^{r-1}(p - 1)(q - 1) + 1, \\ &\vdots \\ e_n d_n &= k_n p^{r-1}(p - 1)(q - 1) + 1, \end{aligned} \] 因此，对于未知的 $(d_1, \cdots, d_n)$，我们有以下模方程： \[ \begin{aligned} e_1 d_1 &= k_1 p^{r-1}(p - 1)(q - 1) + 1, \\ e_2 d_2 &= k_2 p^{r-1}(p - 1)(q - 1) + 1, \\ &\vdots \\ e_n d_n &= k_n p^{r-1}(p - 1)(q - 1) + 1, \end{aligned} \] 正如所示，$(d_1, d_2, \cdots, d_n)$ 是以未知除数为模的联立模单变量线性方程的根，并且其大小受到限制，即 $d_l \leq N^\delta$，对于 $l = 1, \dots, n$。

利用中的技术，可以证明如果 \[ \delta < \frac{(r - 1)}{(r + 1)} \cdot \frac{n}{n + 1} \] 在假设1下，这些联立模线性方程可以被解，这意味着 $(d_1, \cdots, d_n)$ 可以被恢复。然后可以通过计算公因子轻松地分解 $N$。

实验结果. 我们在 Magma 2.11中实现了实验程序。在所有实验中，我们成功地求解了所需的解 $(d_1, d_2, \cdots, d_n)$。同样地，没有实验结果与假设1相矛盾，见表5。

表5. 使用多个解密指数因式分解 $N$。

需要注意的是，前述的定理3可以适用于任意大小的加密指数 $(e_1, \cdots, e_n)$。然而，如果存在两个有效的密钥对 $(e_1, d_1)$ 和 $(e_2, d_2)$，其中 $e_1$ 和 $e_2$ 的大小大致与模 $N$ 或更大些的值如 $N^\alpha$ 相同。假设 $d_1 \simeq d_2 \simeq N^\delta$，则我们可以给出如下分析。

给定两个方程 $e_1 d_1 = k_1 p^{r-1}(p - 1)(q - 1) + 1$ 和 $e_2 d_2 = k_2 p^{r-1}(p - 1)(q - 1) + 1$，我们消除 $p^{r-1}(p - 1)(q - 1)$ 并得到以下等式， \[ k_2 (e_1 d_1 - 1) = k_1 (e_2 d_2 - 1) \] 这启示我们寻找多项式 \[ \begin{equation} f(x, y) = e_2 x + y \pmod{e_1} \end{equation} \] 的小解。

由于 $(d_2 k_1, k_2 - k_1)$ 是 $f(x, y) \pmod{e_1}$ 的根，因此 $k_1$ 的界限可以估计为 $N^{\alpha + \delta - 1}$，因此我们定义边界 $|d_2 k_1| \simeq X = N^{\alpha + 2\delta - 1}$ 和 $|k_2 - k_1| \simeq Y = N^{\alpha + \delta - 1}$。对于这个线性模方程，只要 $XY < e$，或者 $\alpha + 2\delta - 1 + \alpha + \delta - 1 < \alpha$，我们就可以恢复 $(d_2 k_1, k_2 - k_1)$。

因此，要从这个基于格的方法中恢复 $d_2 k_1$ 和 $k_2 - k_1$，加密和解密指数的大小应满足 \[ \alpha + 3\delta < 2 \] 其中 $\alpha + \delta > 1$。

结论

在本文中，我们提出了基于 Minkowski 和的格构造的一些应用，并对多对 CRT-RSA 模数 $N$ 相同的加解密指数对的情况进行了分析。我们展示了当 $d_{p_i}, d_{q_i} \leq N^{\frac{2l - 3}{8l + 2}}$ 或者 $d_{p_i}$ 和 $d_{q_i}$ 中的一个小于 $N^{\frac{9l - 14}{24l + 8}}$ 时，可以分解 $N$，其中 $i = 1, 2, \cdots, l$。此外，我们还分析了在模数为 $N = p^r q$ 的 Takagi 变种 RSA 中使用多个加密和解密指数的情况。

致谢

作者要感谢匿名审稿人对本文的有益评论和建议。本文的工作得到了中国国家重点基础研究计划（项目编号2013CB834203和2011CB302400）、中国国家自然科学基金（项目编号61472417、61402469、61472416和61272478）、中国科学院战略性先导科技专项（项目编号 XDA06010702和 XDA06010703）以及中国科学院信息安全国家重点实验室的支持。Y. Lu 受到 JST 项目 CREST 的支持。

附录

这里给出计算 $S_{X_1}, S_Y, S_{Z_1}, S_{e_1}$ 的细节。

设对于任意 $0 \le a,b \le n$，记 $\sum^*$ 表示 $\sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{j_1=0}^{m-i_1} \cdots \sum_{j_n=0}^{m-i_n}$。我们有

\[ \sum^* i_a i_b = \begin{cases} \frac{1}{12 \cdot 2^{n-1}} \cdot m^{2n+2} + o(m^{2n+2}), & (a = b), \\ \frac{1}{18 \cdot 2^{n-1}} \cdot m^{2n+2} + o(m^{2n+2}), & (a \ne b), \end{cases} \]

和

\[ \sum^\star i_a j_b = \begin{cases} \frac{1}{24 \cdot 2^{n-1}} \cdot m^{2n+2} + o(m^{2n+2}), & (a = b), \\ \frac{1}{18 \cdot 2^{n-1}} \cdot m^{2n+2} + o(m^{2n+2}), & (a \ne b). \end{cases} \]

然后我们得到 \[ \begin{align*} \sum^* \sum_{k=0}^{i_1+\cdots+i_n} i_1 + \cdots + i_n &= \left( \frac{n^2}{18} + \frac{n}{36} \right) \cdot \frac{m^{2n+2}}{2^{n-1}} + o(m^{2n+2}), \\ \sum^*\sum_{k=0}^{i_1+\cdots+i_n} j_1 + \cdots + j_n &= \left( \frac{n^2}{18} - \frac{n}{72} \right) \cdot \frac{m^{2n+2}}{2^{n-1}} + o(m^{2n+2}), \\ \sum^* \sum_{k=0}^{i_1+\cdots+i_n} k &= \sum^*\left( \frac{(i_1+\cdots+i_n)^2}{2} + \frac{i_1+\cdots+i_n}{2} \right) \\ &= \left( \frac{n^2}{36} + \frac{n}{72} \right) \cdot \frac{m^{2n+2}}{2^{n-1}} + o(m^{2n+2}). \end{align*} \] 此外， \[ \begin{align*} \sum^* \sum_{k=0}^{i_1+\cdots+i_n} \min(i_1, k) &= \sum^*\left( \sum_{k=0}^{i_1} k + \sum_{k=i_1+1}^{i_1+\cdots+i_n} i_1 \right) \\ &= \sum^* \left( \frac{i_1(i_1+1)}{2} + i_1(i_2+\cdots+i_n) \right) \\ &= \left( \frac{n}{18} - \frac{1}{72} \right) \cdot \frac{m^{2n+2}}{2^{n-1}} + o(m^{2n+2}). \end{align*} \] 通过对称，我们有

\[ \sum^* \sum_{k=0}^{i_1+\cdots+i_n} \min(i_1, k) + \cdots + \min(i_n, k) = \left( \frac{n^2}{18} - \frac{n}{72} \right) \cdot \frac{m^{2n+2}}{2^{n-1}} + o(m^{2n+2}). \]

格 $L'$ 的维度是

$$ (L’) = ^* _{k=0}^{i_1++i_n} 1 = m^{2n+1} + o(m^{2n+1}).