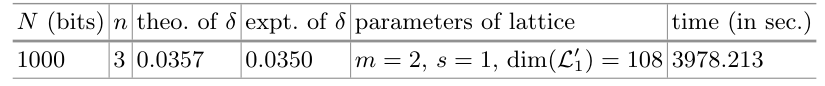原名Cryptanalysis of Variants of RSA with Multiple Small Secret Exponents ,INDOCRYPT 2015。
在本文中,我们分析了 RSA 公钥加密系统的两种变体的安全性,其中使用了多个加密和解密指数,并且这些指数共用一个模数。对于最为知名的变体 CRT-RSA,假设有 n n n ( e l , d p l , d q l ) (e_l, d_{p_l}, d_{ql}) ( e l , d p l , d q l ) l = 1 , … , n l = 1, \ldots , n l = 1 , … , n N N N l = 1 , … , n l = 1, \ldots , n l = 1 , … , n d p l , d q l < N 2 n − 3 8 n + 2 d_{p_l}, d_{ql} < N^\frac{2n-3}{8n+2} d p l , d q l < N 8 n + 2 2 n − 3 l = 1 , … , n l = 1, \ldots , n l = 1 , … , n d p l d_{p_l} d p l d q l d_{ql} d q l < N 9 n − 14 24 n + 8 < N^\frac{9n-14}{24n+8} < N 2 4 n + 8 9 n − 1 4 n n n l = 1 , … , n l = 1, \ldots , n l = 1 , … , n N = p r q N=p^rq N = p r q l = 1 , ⋯ , n l = 1, \cdots , n l = 1 , ⋯ , n d l < N ( r − 1 r + 1 ) n + 1 n d_l < N^{\left(\frac{r-1}{r+1}\right)^{\frac{n+1}{n}}} d l < N ( r + 1 r − 1 ) n n + 1 N N N
自从 RSA 公钥方案的发明以来[16],由于其有效的加密和解密,它已被广泛应用。为了获得高效性,一些原始 RSA 的变体被设计出来。Wiener [24]提出了一种算法,在解密阶段使用中国剩余定理来加速解密操作,通过使用满足 e d p ≡ 1 m o d ( p − 1 ) e d_{p}\equiv 1\mathrm{mod}(p-1) e d p ≡ 1 m o d ( p − 1 ) e d q ≡ 1 m o d ( q − 1 ) e d_{q}\equiv 1\mathrm{mod}\left(q-1\right) e d q ≡ 1 m o d ( q − 1 ) d p d_p d p d q d_q d q N = p q N=pq N = p q N = p r q N=p^rq N = p r q r ≥ 2 r ≥ 2 r ≥ 2 e e e d d d e d ≡ 1 ( m o d p r − 1 ( p − 1 ) ( q − 1 ) ) ed \equiv 1 \pmod{p^{r-1}(p - 1)(q - 1)} e d ≡ 1 ( m o d p r − 1 ( p − 1 ) ( q − 1 ) )
在 RSA 方案及其变体的许多应用中,要么选择 d d d d p d_p d p d q d_q d q d d d
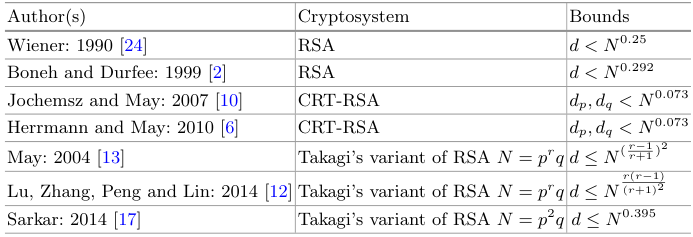
RSA 及其变体的小指数攻击 :对于原始的 RSA,当 d ≤ N 0.25 d \leq N^{0.25} d ≤ N 0 . 2 5 N N N N 0.292 N^{0.292} N 0 . 2 9 2 N 0.292 N^{0.292} N 0 . 2 9 2 N 0.292 N^{0.292} N 0 . 2 9 2 e e e
对于 CRT-RSA,Jochemsz 和 May [10]提出了一种针对小 d p d_p d p d q d_q d q p p p q q q e e e N = p q N = pq N = p q N N N d p d_p d p d q d_q d q N 0.073 N^{0.073} N 0 . 0 7 3
对于具有模数 N = p r q N=p^rq N = p r q d ≤ N ( r − 1 r + 1 ) 2 d \leq N^{(\frac{r-1}{r+1})^2} d ≤ N ( r + 1 r − 1 ) 2 d ≤ N ( r ( r − 1 ) ( r + 1 ) 2 ) d \leq N^{(\frac{r(r-1)}{(r+1)^2})} d ≤ N ( ( r + 1 ) 2 r ( r − 1 ) ) p r q = N p^rq = N p r q = N r ≤ 5 r \leq 5 r ≤ 5 r = 2 r = 2 r = 2 N 0.222 N^{0.222} N 0 . 2 2 2 N 0.395 N^{0.395} N 0 . 3 9 5
多个小秘密指数的 RSA :为了简化 RSA 密钥管理,人们可能会为几个密钥对(e i e_i e i d i d_i d i N N N m m m m m m N N N N N N ( e 1 , ⋯ , e n ) (e_1, \cdots , e_n) ( e 1 , ⋯ , e n ) ( d 1 , ⋯ , d n ) (d_1, \cdots , d_n) ( d 1 , ⋯ , d n ) l = 1 , ⋯ , n l=1,\cdots,n l = 1 , ⋯ , n n n n d l < N δ d_l < N^\delta d l < N δ N N N
δ < { ( 2 n + 1 ) 2 n − ( 2 n + 1 ) ( n n 2 ) ( 2 n − 1 ) 2 n + ( 4 n + 2 ) ( n n 2 ) , 若 n 为奇数 , ( 2 n + 1 ) 2 n − 4 n ( n − 1 n − 1 2 ) ( 2 n − 2 ) 2 2 n + 8 n ( n − 1 n − 1 2 ) , 若 n 为偶数 , . \delta\lt {\left\{
\begin{array}{l l}
{\frac{(2n+1)2^{n}-(2n+1){\binom{n}{\frac{n}{2}}}}{(2n-1)2^{n}+(4n+2){\binom{n}{\frac{n}{2}}}}},{\text{~若~}}n{\text{~为奇数}},\\
{\frac{(2n+1)2^{n}-4n{\binom{n-1}{\frac{n-1}{2}}}}{(2n-2)2^{2^n}+8n{\binom{n-1}{\frac{n-1}{2}}}},{\text{~若~}}n{\text{~为偶数}},.}
\end{array}\right.} δ < ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ ( 2 n − 1 ) 2 n + ( 4 n + 2 ) ( 2 n n ) ( 2 n + 1 ) 2 n − ( 2 n + 1 ) ( 2 n n ) , 若 n 为奇数 , ( 2 n − 2 ) 2 2 n + 8 n ( 2 n − 1 n − 1 ) ( 2 n + 1 ) 2 n − 4 n ( 2 n − 1 n − 1 ) , 若 n 为偶数 , .
N N N
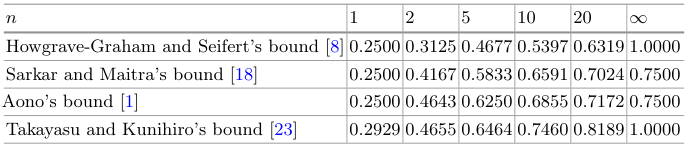
在[18]中,Sarkar 和 Maitra采用了[9]中的策略来解决一个整数方程的小根,并将界限提高到了 δ < 3 n − 1 ( 4 n + 4 ) \delta < \frac{3n-1}{ (4n+4)} δ < ( 4 n + 4 ) 3 n − 1 δ < 9 n − 5 12 n + 4 \delta < \frac{9n-5}{12n+4}
δ < 1 2 n + 4 9 n − 5 N N N 1 − 2 3 n + 1 1 - \sqrt{\frac{2}{3n+1}} 1 − 3 n + 1 2
模未知除数的同时模一元线性方程 :2001年,Howgrave-Graham 首次考虑了解决一个未知除数的已知复合整数的模一元线性方程的问题,形式为
f ( x ) = x + a ( m o d p ) f(x) = x + a \pmod{p}
f ( x ) = x + a ( m o d p )
其中 a a a p ≃ N β p \simeq N^\beta p ≃ N β N N N ∣ x ∣ < N δ |x| < N^\delta ∣ x ∣ < N δ δ < β 2 \delta < β^2 δ < β 2
Cohn 和 Heninger [4]考虑了这个问题的一般化:
{ f ( x 1 ) = x 1 + a 1 ( m o d p ) , f ( x 2 ) = x 2 + a 2 ( m o d p ) , ⋅ ⋅ ⋅ f ( x n ) = x n + a n ( m o d p ) . \left\{\begin{array}{l}
{f(x_{1})=x_{1}+a_{1}\,\,(\mathrm{mod}\,p),}\\
{f(x_{2})=x_{2}+a_{2}\,\,(\mathrm{mod}\,p),}\\
{\cdot\cdot\cdot}\\
{f(x_{n})=x_{n}+a_{n}\,\,(\mathrm{mod}\,p).}
\end{array}\right. ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ f ( x 1 ) = x 1 + a 1 ( m o d p ) , f ( x 2 ) = x 2 + a 2 ( m o d p ) , ⋅ ⋅ ⋅ f ( x n ) = x n + a n ( m o d p ) .
在上述的同时模一元线性方程中,a 1 , ⋯ , a n a_1, \cdots , a_n a 1 , ⋯ , a n p ≃ N β p \simeq N^\beta p ≃ N β N N N
γ 1 + ⋅ ⋅ ⋅ + γ n n < β n + 1 n 且 β ≫ 1 log N \frac{\gamma_{1}+\cdot\cdot\cdot+\gamma_{n}}{n}\,\lt \beta^{\frac{n+1}{n}}\,~\text{且}\ \beta \gg \frac{1}{\sqrt{\log N}}
n γ 1 + ⋅ ⋅ ⋅ + γ n < β n n + 1 且 β ≫ log N 1
其中 ∣ x 1 ∣ < N γ 1 , … , ∣ x n ∣ < N γ n |x_1| < N^{\gamma_1}, \ldots , |x_n| < N^{\gamma_n} ∣ x 1 ∣ < N γ 1 , … , ∣ x n ∣ < N γ n
\sqrt[n]{\gamma_1 \cdots \gamma_n} < \beta^{\frac{n+1}{n}}
\,~\text{且}\
\beta \gg \frac{1}{\sqrt{\log N}}
我们的贡献 :在本文中,我们分别对 CRT-RSA 和 Takagi 的 RSA 变体进行了多个小解密指数的分析。对于 CRT-RSA,( e 1 , ⋯ , e n ) (e_1, \cdots , e_n) ( e 1 , ⋯ , e n ) n n n ( d p 1 , d q 1 ) , ⋯ , ( d p n , d q n ) (d_{p1}, d_{q1}), \cdots , (d_{pn}, d_{qn}) ( d p 1 , d q 1 ) , ⋯ , ( d p n , d q n ) N N N e 1 , ⋯ , e n e_1, \cdots , e_n e 1 , ⋯ , e n N N N n n n
d p l , d q l < N 2 n − 3 8 n + 2 d_{pl}, d_{ql} < N^{\frac{2n-3}{8n+2}}
d p l , d q l < N 8 n + 2 2 n − 3
为了利用基于 Minkowski 求和的格构造来合并方程,这些方程应该共享一个公共变量。因此,我们修改了[10]中考虑的每个方程,当只有一对加密和解密指数时,它们导致了一个更差的界限。
然而,注意到模方程
k p l ( p − 1 ) + 1 ≡ 0 ( m o d e l ) k_{pl}(p - 1) + 1 \equiv 0 \pmod{e_l}
k p l ( p − 1 ) + 1 ≡ 0 ( m o d e l )
对于 l = 1 , … , n l = 1, \ldots , n l = 1 , … , n p p p n n n q q q d p l < N 9 n − 14 24 n + 8 d_{pl} < N^\frac{9n-14}{24n+8} d p l < N 2 4 n + 8 9 n − 1 4
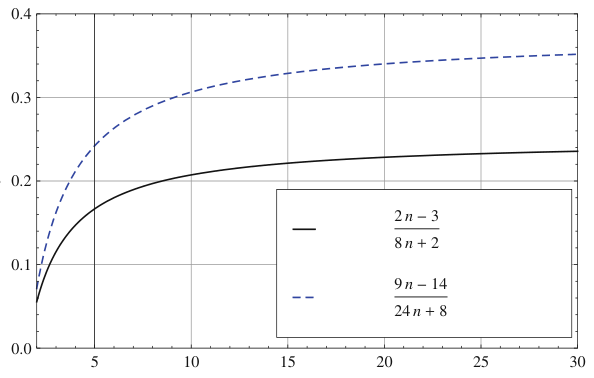
需要注意的是,为了组合这些方程,我们修改了[10]中考虑的每个方程。当有 n = 2 n = 2 n = 2 N 0.071 N^{0.071} N 0 . 0 7 1 N 0.073 N^{0.073} N 0 . 0 7 3 n ≥ 3 n ≥ 3 n ≥ 3 N 0 . 375 N^0.375 N 0 . 3 7 5 d p l < N 0.035 d_{pl} < N^{0.035} d p l < N 0 . 0 3 5 N N N N 0 . 015 N^0.015 N 0 . 0 1 5 N 0 . 029 N^0.029 N 0 . 0 2 9
这些界限的明确描述如图1所示。
d p l d_{pl} d p l d q l d_{ql} d q l n n n d p l d_{pl} d p l n n n
对于 Takagi 的 RSA 变体,假设存在 n n n ( e l , d l ) (e_l, d_l) ( e l , d l ) N = p r q N=p^rq N = p r q l l l d l ≤ N δ d_l \leq N^\delta d l ≤ N δ
δ < ( r − 1 r + 1 ) ( n + 1 ) n \delta < \left(\frac{r - 1}{r + 1}\right) ^ \frac{(n+1)}{n}
δ < ( r + 1 r − 1 ) n ( n + 1 )
本文的其余部分安排如下。第2节是关于格和 CRT-RSA 变体的一些初步知识。在第3节中,我们分析了具有多个小解密指数的 CRT-RSA。第4节介绍了对具有多个小解密指数的 Takagi 的变体 RSA 的分析。最后,第5节是结论。
让 w 1 , w 2 , ⋯ , w k w_1, w_2, \cdots , w_k w 1 , w 2 , ⋯ , w k n n n R n \mathbb{R}^{n} R n k k k w 1 , ⋯ , w k {w_1, \cdots , w_k} w 1 , ⋯ , w k L \mathcal{L} L w 1 , ⋯ , w k w_1, \cdots , w_k w 1 , ⋯ , w k c 1 w 1 + ⋯ + c k w k c_1w_1 + \cdots + c_kw_k c 1 w 1 + ⋯ + c k w k c 1 , … , c k ∈ Z c_1, \ldots , c_k \in \mathbb{Z} c 1 , … , c k ∈ Z k k k L \mathcal{L} L R n \mathbb{R}^{n} R n w 1 , ⋯ , w k {w_1, \cdots , w_k} w 1 , ⋯ , w k L \mathcal{L} L ± 1 ±1 ± 1 1 1 1
Lenstra 等人[11]引入了著名的 L 3 L^3 L 3 L 3 L^3 L 3
引理1 (L 3 L^3 L 3 L \mathcal{L} L k k k L 3 L^3 L 3 L \mathcal{L} L v 1 , … , v k v_1, \ldots , v_k v 1 , … , v k
∥ v i ∥ ≤ 2 k ( k − i ) 4 ( k + 1 − i ) ⋅ det ( L ) 1 k + 1 − i \lVert v_i \rVert \leq 2^\frac{k(k-i)}{4(k+1-i)} \cdot \det({\mathcal{L}})^\frac{1}{k+1-i}
∥ v i ∥ ≤ 2 4 ( k + 1 − i ) k ( k − i ) ⋅ det ( L ) k + 1 − i 1
,对于任意 1 ≤ i ≤ k 1 \leq i \leq k 1 ≤ i ≤ k
Coppersmith [5]应用 L 3 L^3 L 3
对于给定的多项式 g ( x 1 , ⋯ , x k ) = ∑ ( i 1 , … , i k ) a i 1 , … , i k x 1 i 1 ⋯ x k i k g(x_1, \cdots , x_k) = \sum_{(i_1,\ldots,i_k)} a_{i_1,\ldots,i_k}x^{i_1}_1 \cdots x^{i_k}_{k} g ( x 1 , ⋯ , x k ) = ∑ ( i 1 , … , i k ) a i 1 , … , i k x 1 i 1 ⋯ x k i k g g g
∥ g ( x 1 , … , x k ) ∥ = ( ∑ ( i 1 , … , i k ) a i 1 , … , i k 2 ) 1 2 \lVert g(x_1, \ldots , x_k) \rVert = \left( \sum_{(i_1,\ldots,i_k)} a_{i_1,\ldots,i_k}^2 \right)^{\frac{1}{2}}
∥ g ( x 1 , … , x k ) ∥ = ⎝ ⎛ ( i 1 , … , i k ) ∑ a i 1 , … , i k 2 ⎠ ⎞ 2 1
Howgrave-Graham [7]的以下引理给出了将模方程转换为整数方程的一个充分条件。
引理2 (Howgrave-Graham,[7])。设 g ( x 1 , … , x k ) ∈ Z [ x 1 , … , x k ] g(x_1, \ldots , x_k) \in \mathbb{Z}[x_1, \ldots , x_k] g ( x 1 , … , x k ) ∈ Z [ x 1 , … , x k ] w w w
g ( y 1 , ⋯ , y k ) ≡ 0 ( m o d p m ) 对于成立 ∣ y 1 ∣ ≤ X 1 , ⋯ , ∣ y k ∣ ≤ X k 并且 ∥ g ( x 1 X 1 , … , x k X k ) ∥ < p m w \begin{aligned}
&g(y_1, \cdots , y_k) \equiv 0 \pmod{p^m} \text{对于成立} |y_1| \leq X_1, \cdots , |y_k| \leq X_k\text{并且}\\
&\lVert g(x_1X_1, \ldots , x_kX_k) \rVert < \frac{p^m}{\sqrt{w}}
\end{aligned} g ( y 1 , ⋯ , y k ) ≡ 0 ( m o d p m ) 对于成立 ∣ y 1 ∣ ≤ X 1 , ⋯ , ∣ y k ∣ ≤ X k 并且 ∥ g ( x 1 X 1 , … , x k X k ) ∥ < w p m
那么在整数域上g ( y 1 , … , y k ) = 0 g(y_1, \ldots , y_k) = 0 g ( y 1 , … , y k ) = 0
假设我们有 w ( > k ) w(> k) w ( > k ) b 1 , … , b w b_1, \ldots , b_w b 1 , … , b w x 1 , … , x k x_1, \ldots , x_k x 1 , … , x k b 1 ( y 1 , … , y k ) = ⋯ = b w ( y 1 , … , y k ) = 0 ( m o d p m ) b_1(y_1, \ldots , y_k) = \cdots = b_w(y_1, \ldots , y_k) = 0 \pmod{p^m} b 1 ( y 1 , … , y k ) = ⋯ = b w ( y 1 , … , y k ) = 0 ( m o d p m ) ∣ y 1 ∣ ≤ X 1 , … , ∣ y k ∣ ≤ X k |y_1| \leq X_1, \ldots , |y_k| \leq X_k ∣ y 1 ∣ ≤ X 1 , … , ∣ y k ∣ ≤ X k b 1 ( x 1 X 1 , … , x k X k ) , … , b w ( x 1 X 1 , … , x k X k ) b_1(x_1X_1, \ldots , x_kX_k), \ldots , b_w(x_1X_1, \ldots , x_kX_k) b 1 ( x 1 X 1 , … , x k X k ) , … , b w ( x 1 X 1 , … , x k X k ) L \mathcal{L} L k k k v 1 ( x 1 , … , x k ) , … , v k ( x 1 , … , x k ) v_1(x_1, \ldots , x_k), \ldots , v_k(x_1, \ldots , x_k) v 1 ( x 1 , … , x k ) , … , v k ( x 1 , … , x k )
v 1 ( y 1 , … , y k ) = ⋯ = v k ( y 1 , … , y k ) = 0 ( m o d p m ) v_1(y_1, \ldots , y_k) = \cdots = v_k(y_1, \ldots , y_k) = 0 \pmod{p^m}
v 1 ( y 1 , … , y k ) = ⋯ = v k ( y 1 , … , y k ) = 0 ( m o d p m )
它们对应于约简基的前 k k k L 3 L^3 L 3
∥ v 1 ( x 1 X 1 , … , x k X k ) ∥ ≤ ⋯ ≤ ∥ v k ( x 1 X 1 , … , x k X k ) ∥ ≤ 2 w ( w − 1 ) 4 ( w + 1 − k ) det ( L ) 1 w + 1 − k . \lVert v_1(x_1X_1, \ldots , x_kX_k) \rVert \leq \cdots \leq \lVert v_k(x_1X_1, \ldots , x_kX_k) \rVert \leq 2^\frac{w(w-1)}{4(w+1-k)}\det(\mathcal{L}) ^ \frac{1}{w+1-k}.
∥ v 1 ( x 1 X 1 , … , x k X k ) ∥ ≤ ⋯ ≤ ∥ v k ( x 1 X 1 , … , x k X k ) ∥ ≤ 2 4 ( w + 1 − k ) w ( w − 1 ) det ( L ) w + 1 − k 1 .
因此根据引理2,如果
2 w ( w − 1 ) 4 ( w + 1 − k ) ⋅ det ( L ) 1 w + 1 − k < p m w 2^{\frac{w(w-1)}{4(w+1-k)}} \cdot \det({\mathcal{L}})^{\frac{1}{w+1-k}} < \frac{p^m}{ \sqrt{w}}
2 4 ( w + 1 − k ) w ( w − 1 ) ⋅ det ( L ) w + 1 − k 1 < w p m
那么我们有 v 1 ( y 1 , … , y k ) = ⋯ = v k ( y 1 , … , y k ) = 0 v_1(y_1, \ldots , y_k) = \cdots = v_k(y_1, \ldots , y_k) = 0 v 1 ( y 1 , … , y k ) = ⋯ = v k ( y 1 , … , y k ) = 0 v 1 , … , v k v_1, \ldots , v_k v 1 , … , v k y 1 , … , y k y_1, \ldots , y_k y 1 , … , y k
一旦我们从 L 3 L^3 L 3
假设1 :我们基于格的构造产生了代数无关的多项式。这些多项式的公共根可以通过计算resultant或找到Gröbner基等技术来高效地计算。
与其他格约简工作类似[1,9,10,23],虽然我们提供了实验结果支持我们的攻击,但我们也想指出理论结果是渐近的,因为我们在攻击计算中在某些情况下忽略了常数。
基于 Minkowski 求和的格构造 。在[1]中,Aono 提出了一种用于同时模方程 Coppersmith 技术的格构造方法。为了阐明这一点,让我们通过一个例子来说明。假设有两个模方程 f 1 ≡ 0 ( m o d W 1 ) f_1 \equiv 0 \pmod{W_1} f 1 ≡ 0 ( m o d W 1 ) f 2 ≡ 0 ( m o d W 2 ) f_2 \equiv 0 \pmod{W_2} f 2 ≡ 0 ( m o d W 2 ) f 1 f_1 f 1 g 1 , … , g n g_1, \ldots , g_n g 1 , … , g n W 1 m W^m_1 W 1 m g 1 ′ , … , g n ′ g'_1, \ldots , g'_n g 1 ′ , … , g n ′ W 2 m W^m_2 W 2 m g i g j ′ g_i g'_j g i g j ′ 1 ≤ i , j ≤ n 1 \leq i,j \leq n 1 ≤ i , j ≤ n W 1 m W 2 m W^m_1 W^m_2 W 1 m W 2 m W 1 m W 2 m W^m_1 W^m_2 W 1 m W 2 m ∑ i , j a i , j g i g j ′ \sum_{i,j} a_{i,j} g_i g'_j ∑ i , j a i , j g i g j ′ a i , j a_{i,j} a i , j g 1 , … , g n g_1, \ldots , g_n g 1 , … , g n g 1 ′ , … , g n ′ g'_1, \ldots , g'_n g 1 ′ , … , g n ′
CRT-RSA ,即中国剩余定理 RSA,是 RSA 公钥加密系统的一种变体。自从 RSA 公钥加密系统的发明以来,由于其简洁有效的加密和解密方式,该公钥方案已被广泛应用。Wiener [24] 提出在解密阶段使用中国剩余定理。这个方案通常被称为 CRT-RSA。基于 Sun 和 Wu 的工作 [20],这个变体的一个版本可以描述如下:
在 CRT-RSA 的密钥生成算法中描述了这样一种情况:可能存在多个有效的加密和解密指数对应于相同的 CRT-RSA 模 N = p q N = pq N = p q ( p , q ) (p, q) ( p , q ) d p d_p d p d q d_q d q
在这一部分,沿用[1,8,18,23]的思路,我们给出了以下定理,用于描述当多个加密和解密指数用于一个公共的 CRT-RSA 模时的情况。通过将我们的结果与 Jochemsz 和 May 的结果[10]进行比较,我们改进了在一个公共的 CRT-RSA 模中存在 3 3 3 N 0.015 N^{0.015} N 0 . 0 1 5 N 0.029 N^{0.029} N 0 . 0 2 9 N 0.035 N^{0.035} N 0 . 0 3 5
定理1. 设 ( e 1 , e 2 , … , e n ) (e_1, e_2, \ldots , e_n) ( e 1 , e 2 , … , e n ) n n n N = p q N= pq N = p q n ≥ 3 n ≥ 3 n ≥ 3 e 1 , e 2 , … , e n e_1, e_2, \ldots , e_n e 1 , e 2 , … , e n N N N d p i , d q i ≤ N δ d_{p_i}, d_{q_i} \leq N^\delta d p i , d q i ≤ N δ i = 1 , 2 , … , n i = 1, 2, \ldots , n i = 1 , 2 , … , n 假设1 ,在
δ < 2 n − 3 8 n + 2 \delta < \frac{2n - 3}{8n + 2}
δ < 8 n + 2 2 n − 3
时,可以在多项式时间内分解 N N N
证明. 对于一对密钥 ( e l , d p l , d q l ) (e_l, d_{pl}, d_{ql}) ( e l , d p l , d q l )
e l d p l − 1 ≡ k p l ( p − 1 ) e l d p l − 1 ≡ k q l ( q − 1 ) e_{l}d_{pl} - 1 \equiv k_{pl}(p - 1)\\
e_{l}d_{pl} - 1 \equiv k_{ql}(q - 1) e l d p l − 1 ≡ k p l ( p − 1 ) e l d p l − 1 ≡ k q l ( q − 1 )
其中 k p l k_{pl} k p l k q l k_{ql} k q l
此外,通过将这两个方程相乘,我们有
e l 2 d p l d q l − e l ( d p l + d q l ) + 1 = k p l k q l ( N − s ) e^2_ld_{pl}d_{ql} - e_l(d_{pl} + d_{ql}) + 1 = k_{pl}k_{ql}(N - s)
e l 2 d p l d q l − e l ( d p l + d q l ) + 1 = k p l k q l ( N − s )
其中 s = p + q − 1 s = p + q - 1 s = p + q − 1
那么 ( k p l k q l , s , d p l + d q l ) (k_{pl}k_{ql}, s, d_{pl} + d_{ql}) ( k p l k q l , s , d p l + d q l )
f l ( x l , y , z l ) = x l ( N − y ) + e l z l − 1 ( m o d e l 2 ) f_l(x_l, y, z_l) = x_l(N - y) + e_lz_l - 1 \pmod{e^2_l}
f l ( x l , y , z l ) = x l ( N − y ) + e l z l − 1 ( m o d e l 2 )
的一个解。
此外,考虑 n n n
\begin{equation}
f_l(x_l, y, z_l) = x_l(N - y) + e_lz_l - 1 \pmod{e^{2l}}
\end{equation}
其中 l = 1 , … , n l = 1, \ldots , n l = 1 , … , n
这些多项式有一个公共的根 ( x 1 , … , x n , y , z 1 , … , z n ) = ( k p 1 k q 1 , … , k p n k q n , s , d p 1 + d q 1 , … , d p n + d q n ) (x_1, \ldots , x_n, y, z_1, \ldots , z_n) = (k_{p_1}k_{q_1}, \ldots , k_{p_n}k_{q_n}, s, d_{p_1} + d_{q_1}, \ldots , d_{p_n} + d_{q_n}) ( x 1 , … , x n , y , z 1 , … , z n ) = ( k p 1 k q 1 , … , k p n k q n , s , d p 1 + d q 1 , … , d p n + d q n ) k p l k q l ≃ X l = N 1 + 2 δ k_{p_l}k_{q_l} \simeq X_l = N^{1 + 2\delta} k p l k q l ≃ X l = N 1 + 2 δ s ≃ Y = N 1 / 2 s \simeq Y = N^{1/2} s ≃ Y = N 1 / 2 d p l + d q l ≃ N δ = Z d_{pl} + d_{ql} \simeq N^\delta = Z d p l + d q l ≃ N δ = Z l = 1 , … , n l = 1, \ldots , n l = 1 , … , n
为了解决模多项式 f l ( x l , y , z l ) = 0 ( m o d e l 2 ) f_l(x_l, y, z_l) = 0 \pmod{e^2_l} f l ( x l , y , z l ) = 0 ( m o d e l 2 ) l = 1 , … , n l = 1, \ldots , n l = 1 , … , n
S l = { x l i l z l j l f l k l ( x l , y , z l ) ( e l 2 ) m − k l ∣ 0 ≤ k l ≤ m , 0 ≤ i l ≤ m − k l , 0 ≤ j l ≤ m − i l − k l } S_l = \{ x_l^{i_l} z_l^{j_l} f_l^{k_l} (x_l, y, z_l) (e^2_l)^{m - k_l} \, | \, 0 \leq k_l \leq m, 0 \leq i_l \leq m - k_l, 0 \leq j_l \leq m - i_l - k_l \}
S l = { x l i l z l j l f l k l ( x l , y , z l ) ( e l 2 ) m − k l ∣ 0 ≤ k l ≤ m , 0 ≤ i l ≤ m − k l , 0 ≤ j l ≤ m − i l − k l }
其中 l = 1 , … , n l = 1, \ldots , n l = 1 , … , n m m m
每次(1)中对应方程的选择都会生成一个三角形基矩阵。同样地,对于每个 l = 1 , 2 , … , n l = 1, 2, \ldots , n l = 1 , 2 , … , n n n n n n n L ′ \mathcal{L}' L ′ ( e 1 2 , … , e n 2 ) m (e^2_1, \ldots , e^2_n)^m ( e 1 2 , … , e n 2 ) m
X 1 i 1 ⋯ X n i n Y k Z 1 j 1 ⋯ Z n j n ( e 1 2 ) m − min ( i 1 , k ) ⋯ ( e n 2 ) m − min ( i n , k ) X^{i_1}_1 \cdots X^{i_n}_n Y^k Z^{j_1}_1 \cdots Z^{j_n}_n (e^2_1)^{m - \min(i_1,k)} \cdots (e^2_n)^{m - \min(i_n,k)}
X 1 i 1 ⋯ X n i n Y k Z 1 j 1 ⋯ Z n j n ( e 1 2 ) m − m i n ( i 1 , k ) ⋯ ( e n 2 ) m − m i n ( i n , k )
其中
\begin{align*}
&0 \leq i_1, \ldots , i_n \leq m, \\
&0 \leq k \leq i_1 + i_2 + \cdots + i_n, \\
&0 \leq j_1 \leq i_1, \ldots , 0 \leq j_n \leq i_n。
\end{align*}
然后,格的行列式可以计算如下,
det ( L ′ ) = ∏ i 1 = 0 m ⋯ ∏ i n = 0 m ∏ k = 0 i 1 + ⋯ + i n ∏ j 1 = 0 m − i 1 ⋯ ∏ j n = 0 m − i n ( X 1 i 1 ⋯ X n i n Y k Z 1 j 1 ⋯ Z n j n ( e 2 1 ) m − min ( i 1 , k ) ⋯ ( e n 2 ) m − min ( i n , k ) ) = X 1 S x 1 ⋯ X n S x n Y S y Z 1 S z 1 ⋯ Z n S z n ( e 1 2 ) S e 1 ⋯ ( e n 2 ) S e n \begin{aligned}
\det({\mathcal{L}}') &=\prod_{i_1=0}^{m} \cdots \prod_{i_n=0}^{m} \prod_{k=0}^{i_1 + \cdots + i_n} \prod_{j_1=0}^{m-i_1} \cdots \prod_{j_n=0}^{m-i_n}\left( X_1^{i_{1}} \cdots X^{i_n}_n Y^k Z^{j_1}_1 \cdots Z^{j_n}_n
(e^{2_1})^{m - \min(i_1,k)} \cdots (e^2_n)^{m - \min(i_n,k)} \right)\\
&= X^1 S^{x_1} \cdots X_n^{S_{x_n}} Y^{S_y }Z^{S_{z_1}}_1 \cdots Z_n^{S_{z_n}} (e^2_1)^{S_{e_1}} \cdots (e^2_n)^{S_{e_n}}
\end{aligned} det ( L ′ ) = i 1 = 0 ∏ m ⋯ i n = 0 ∏ m k = 0 ∏ i 1 + ⋯ + i n j 1 = 0 ∏ m − i 1 ⋯ j n = 0 ∏ m − i n ( X 1 i 1 ⋯ X n i n Y k Z 1 j 1 ⋯ Z n j n ( e 2 1 ) m − m i n ( i 1 , k ) ⋯ ( e n 2 ) m − m i n ( i n , k ) ) = X 1 S x 1 ⋯ X n S x n Y S y Z 1 S z 1 ⋯ Z n S z n ( e 1 2 ) S e 1 ⋯ ( e n 2 ) S e n
其中
\begin{align*}
S_{x_1} + S_{x_2} + \cdots + S_{x_n} = \left( \frac{n^2}{18} + \frac{n}{36} \right) \frac{m^{2n+2}} {2^{n-1} }+ o(m^{2n+2})\\
S_y = \left( \frac{n^2}{36} + \frac{n}{72} \right) \frac{m^{2n+2}} {2^{n-1}} + o(m^{2n+2})\\
S_{z_1} + S_{z_2} + \cdots + S_{z_n} = \left( \frac{n^2}{18} - \frac{n}{72} \right) \frac{m^{2n+2}}{ 2^{n-1} }+ o(m^{2n+2})\\
S_{e_1} + S_{e_2} + \cdots + S_{e_n} = \left( \frac{n^2}{9} - \frac{n}{72} \right) \frac{m^{2n+2}}{ 2^{n-1}} + o(m^{2n+2})
\end{align*}
另一方面,维数为
dim ( L ′ ) = ∑ i 1 = 0 m ⋯ ∑ i n = 0 m ∑ k = 0 i 1 + ⋯ + i n ∑ j 1 = 0 m − i 1 ⋯ ∑ j n = 0 m − i n 1 = n 6 ⋅ 2 n − 1 m 2 n + 1 + o ( m 2 n + 1 ) \text{dim}({\mathcal{L}}') = \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{k=0}^{i_1 + \cdots + i_n} \sum_{j_1=0}^{m-i_1} \cdots \sum_{j_n=0}^{m-i_n} 1 = \frac{n}{6 \cdot 2^{n-1}} m^{2n+1} + o(m^{2n+1})
dim ( L ′ ) = i 1 = 0 ∑ m ⋯ i n = 0 ∑ m k = 0 ∑ i 1 + ⋯ + i n j 1 = 0 ∑ m − i 1 ⋯ j n = 0 ∑ m − i n 1 = 6 ⋅ 2 n − 1 n m 2 n + 1 + o ( m 2 n + 1 )
通过引用引理1和引理2,我们可以得到整数方程,当
\begin{equation}
\det({\mathcal{L}}') ^ \frac{1}{\text{dim}({\mathcal{L}}')} < (e^2_1\cdots e^2_n)^m
\end{equation}
忽略 m m m X l = N 1 + 2 δ X_l = N^{1+2\delta} X l = N 1 + 2 δ Y = N 1 2 Y = N^{\frac{1}{2}} Y = N 2 1 Z l = N δ Z_l = N^{\delta} Z l = N δ e 2 l ≃ N 2 e^{2_l} \simeq N^2 e 2 l ≃ N 2 l = 1 , … , n l = 1, \ldots , n l = 1 , … , n
( 1 + 2 δ ) ( n 2 18 + n 36 ) + 1 2 ( n 2 36 + n 72 ) + δ ( n 2 18 − n 72 ) + 2 ( n 2 9 + n 72 ) ≤ n 2 3 (1 + 2\delta)\left(\frac{n^2}{18} + \frac{n}{36}\right) + \frac{1}{2}\left(\frac{n^2}{36} + \frac{n}{72}\right) + \delta\left(\frac{n^2}{18} - \frac{n}{72}\right) + 2\left(\frac{n^2}{9} + \frac{n}{72}\right) \leq \frac{n^2}{3}
( 1 + 2 δ ) ( 1 8 n 2 + 3 6 n ) + 2 1 ( 3 6 n 2 + 7 2 n ) + δ ( 1 8 n 2 − 7 2 n ) + 2 ( 9 n 2 + 7 2 n ) ≤ 3 n 2
即,
δ < 2 n − 3 8 n + 2 \delta < \frac{2n - 3}{8n + 2}
δ < 8 n + 2 2 n − 3
然后我们得到了 2 n + 1 2n + 1 2 n + 1 ( x 1 , … , x n , y , z 1 , … , z n ) (x_1, \ldots , x_n, y, z_1, \ldots , z_n) ( x 1 , … , x n , y , z 1 , … , z n ) x 1 , … , x n , y , z 1 , … , z n x_1, \ldots , x_n, y, z_1, \ldots , z_n x 1 , … , x n , y , z 1 , … , z n
此外,除了通过 Minkowski 求和格构造来组合多项式e l d p l = k p l ( p − 1 ) + 1 e_ld_{pl} = k_{pl}(p-1)+1 e l d p l = k p l ( p − 1 ) + 1 l = 1 , … , n l = 1, \ldots , n l = 1 , … , n q q q
更具体地说,我们首先通过利用 Minkowski 求和格构造来组合多项式f l ( x l , y ) = x l ( y − 1 ) + 1 ( m o d e l ) f_l(x_l, y) = x_l(y - 1) + 1 \ \pmod {e_l} f l ( x l , y ) = x l ( y − 1 ) + 1 ( m o d e l ) l = 1 , … , n l = 1, \ldots , n l = 1 , … , n y y y p p p N N N q q q z z z p q = N pq = N p q = N N N N y z yz y z N N N e 1 ⋯ e n e_1 \cdots e_n e 1 ⋯ e n
定理2. 设 ( e 1 , e 2 , … , e n ) (e_1, e_2, \ldots , e_n) ( e 1 , e 2 , … , e n ) n n n N = p q N= pq N = p q n ≥ 2 n \geq 2 n ≥ 2 e 1 , e 2 , … , e n e_1, e_2, \ldots , e_n e 1 , e 2 , … , e n N N N d p l d_{p_l} d p l d q l d_{q_l} d q l l = 1 , 2 , … , n l = 1, 2, \ldots , n l = 1 , 2 , … , n l = 1 , 2 , … , n l = 1, 2, \ldots , n l = 1 , 2 , … , n d p l < N δ d_{p_l} < N^\delta d p l < N δ 假设1 下,当
δ < 9 n − 14 24 n + 8 \delta < \frac{9n - 14}{24n + 8}
δ < 2 4 n + 8 9 n − 1 4
时,可以在多项式时间内分解N N N
证明. 对于每对密钥 ( e l , d p l , d q l ) (e_l, d_{p_l}, d_{q_l}) ( e l , d p l , d q l )
e l d p l = k p l ( p − 1 ) + 1 e_ld_{p_l} = k_{p_l}(p - 1) + 1
e l d p l = k p l ( p − 1 ) + 1
其中 k p l k_{p_l} k p l ( k p l , p ) (k_{p_l}, p) ( k p l , p )
f l ( x l , y ) = x l ( y − 1 ) + 1 ( m o d e l ) f_l(x_l, y) = x_l(y - 1) + 1 \ \pmod {e_l}
f l ( x l , y ) = x l ( y − 1 ) + 1 ( m o d e l )
的解。n n n
f l ( x l , y ) = x l ( y − 1 ) + 1 ( m o d e l ) f_l(x_l, y) = x_l(y - 1) + 1 \ \pmod {e_l}
f l ( x l , y ) = x l ( y − 1 ) + 1 ( m o d e l )
其中 l = 1 , … , n l = 1, \ldots , n l = 1 , … , n ( x 1 , … , x n , y ) = ( k p 1 , … , k p n , p ) (x_1, \ldots , x_n, y) = (k_{p_1}, \ldots , k_{p_n}, p) ( x 1 , … , x n , y ) = ( k p 1 , … , k p n , p ) k p l ≃ X l = N 1 2 + δ k_{p_l} \simeq X_l = N^{\frac{1}{2} + \delta} k p l ≃ X l = N 2 1 + δ l = 1 , … , n l = 1, \ldots , n l = 1 , … , n p ≃ Y = N 1 2 p \simeq Y = N^\frac{1}{2} p ≃ Y = N 2 1
为了求解所需解,我们首先选择了以下一组多项式来解决每个单一的模方程,
S l = { x l i l f l k l ( x l , y ) ( e l ) m − k l ∣ 0 ≤ k l ≤ m , 0 ≤ i l ≤ m − k l } S_l = \{ x^{i_l}_{l} f^{k_l}_{l} (x_l, y)(e_l)^{m-k_l} \ | \ 0 \leq k_l \leq m, 0 \leq i_l \leq m - k_l \}
S l = { x l i l f l k l ( x l , y ) ( e l ) m − k l ∣ 0 ≤ k l ≤ m , 0 ≤ i l ≤ m − k l }
其中 l = 1 , … , n l = 1, \ldots , n l = 1 , … , n m m m
每个选择都生成一个三角基矩阵。然后,对于 l = 1 , … , n l = 1, \ldots , n l = 1 , … , n ( e 1 ⋯ e n ) m (e_1 \cdots e_n)m ( e 1 ⋯ e n ) m n n n \mathcal{L}^'_1
X 1 i 1 ⋯ X n i n Y k ( e 1 2 ) m − min ( i 1 , k ) ⋯ e n m − min ( i n , k ) X^{i_1}_1 \cdots X^{i_n}_n Y^k (e^2_1)^{m - \min(i_1,k)} \cdots e_n^{m - \min(i_n,k)}
X 1 i 1 ⋯ X n i n Y k ( e 1 2 ) m − m i n ( i 1 , k ) ⋯ e n m − m i n ( i n , k )
,0 ≤ i 1 , ⋯ , i n ≤ m 0 \leq i_1, \cdots , i_n \leq m 0 ≤ i 1 , ⋯ , i n ≤ m 0 ≤ k ≤ i 1 + i 2 + ⋯ + i n 0 \leq k \leq i_1 + i_2 + \cdots + i_n 0 ≤ k ≤ i 1 + i 2 + ⋯ + i n
此外,注意到所需的小解包含质因数 p p p N = p q N= pq N = p q z z z q q q \mathcal{L}^'_1 中每个行向量对应的多项式乘以某个待优化的 s s s z s z^s z s N N N y z yz y z N = p q N = pq N = p q x 1 i 1 ⋯ x n i n y k z s x_1^{i_1} \cdots x_n^{i_n} y^k z^s x 1 i 1 ⋯ x n i n y k z s k ≥ s k \geq s k ≥ s a i 1 , ⋅ ⋅ ⋅ , i n , k a_{i_1,··· ,i_n,k} a i 1 , ⋅ ⋅ ⋅ , i n , k x 1 i 1 ⋯ x n i n y k − s x_1^{i_1} \cdots x_n^{i_n} y^{k-s} x 1 i 1 ⋯ x n i n y k − s a i 1 , ⋅ ⋅ ⋅ , i n , k N s a_{i_1,··· ,i_n,k}N^s a i 1 , ⋅ ⋅ ⋅ , i n , k N s k < s k < s k < s a i 1 , ⋅ ⋅ ⋅ , i n , k a_{i_1,··· ,i_n,k} a i 1 , ⋅ ⋅ ⋅ , i n , k x 1 i 1 ⋯ x n i n y k z s x_1^{i_1} \cdots x_n^{i_n} y^k z^s x 1 i 1 ⋯ x n i n y k z s k ≥ s k \geq s k ≥ s x 1 i 1 ⋯ x n i n z s − k x_1^{i_1} \cdots x_n^{i_n} z^{s-k} x 1 i 1 ⋯ x n i n z s − k a i 1 , ⋅ ⋅ ⋅ , i n , k N k a_{i_1,··· ,i_n,k}N^k a i 1 , ⋅ ⋅ ⋅ , i n , k N k Z = N 1 2 Z = N^\frac{1}{2} Z = N 2 1 z z z
为了使格的行列式尽可能小,我们尝试消除对角线条目中, N s N^s N s N k N^k N k ( N , e 1 ⋯ e n ) = 1 (N, e_1 \cdots e_n) = 1 ( N , e 1 ⋯ e n ) = 1 N s N^s N s N k N^k N k ( e 1 ⋯ e n ) m (e_1 \cdots e_n)^m ( e 1 ⋯ e n ) m
det ( L 1 ′ ) = X 1 S x 1 ⋯ X n S x n Y S y Z 1 S z 1 ⋯ e n S e n \text{det}(\mathcal{L}^{\prime}_1) = X_1^{S_{x_1}} \cdots X_n^{S_{x_n}} Y^{S_y} Z_1^{S_{z_1}} \cdots e_n^{S_{e_n}}
det ( L 1 ′ ) = X 1 S x 1 ⋯ X n S x n Y S y Z 1 S z 1 ⋯ e n S e n
其中
S x 1 + S x 2 + ⋯ + S x n = ∑ i 1 = 0 m ⋯ ∑ i n = 0 m ∑ k = 0 i 1 + ⋯ + i n ( i 1 + ⋯ + i n ) , S y = ∑ i 1 = 0 m ⋯ ∑ i n = 0 m ∑ k = s i 1 + ⋯ + i n ( k − s ) , S z = ∑ i 1 = 0 m ⋯ ∑ i n = 0 m ∑ k = 0 s − 1 ( s − k ) , S e 1 + S e 2 + ⋯ + S e n = ∑ i 1 = 0 m ⋯ ∑ i n = 0 m ∑ k = 0 i 1 + ⋯ + i n ( n m − min ( i 1 , k ) − ⋯ − min ( i n , k ) ) \begin{aligned}
S_{x_1} + S_{x_2} + \cdots + S_{x_n} &= \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{k=0}^{i_1 + \cdots + i_n} (i_1 + \cdots + i_n),\\
S_y &= \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{k=s}^{i_1 + \cdots + i_n} (k - s),\\
S_z &= \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{k=0}^{s-1} ( s-k),\\
S_{e_1} + S_{e_2} + \cdots + S_{e_n}&= \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum^{i_1 + \cdots + i_n}_{k=0}(nm - \min(i_1, k) - \cdots - \min(i_n, k))
\end{aligned} S x 1 + S x 2 + ⋯ + S x n S y S z S e 1 + S e 2 + ⋯ + S e n = i 1 = 0 ∑ m ⋯ i n = 0 ∑ m k = 0 ∑ i 1 + ⋯ + i n ( i 1 + ⋯ + i n ) , = i 1 = 0 ∑ m ⋯ i n = 0 ∑ m k = s ∑ i 1 + ⋯ + i n ( k − s ) , = i 1 = 0 ∑ m ⋯ i n = 0 ∑ m k = 0 ∑ s − 1 ( s − k ) , = i 1 = 0 ∑ m ⋯ i n = 0 ∑ m k = 0 ∑ i 1 + ⋯ + i n ( n m − min ( i 1 , k ) − ⋯ − min ( i n , k ) )
由于下式对于任意 0 ≤ a , b ≤ n 0 \leq a, b \leq n 0 ≤ a , b ≤ n
∑ i 1 = 0 m ⋯ ∑ i n = 0 m i a i b = { 1 3 m n + 2 + o ( m n + 2 ) , ( a = b ) , 1 4 m n + 2 + o ( m n + 2 ) , ( a ≠ b ) , \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} i_a i_b =
\begin{cases}
\frac{1}{3}m^{n+2} + o(m^{n+2}), & (a = b), \\
\frac{1}{4}m^{n+2} + o(m^{n+2}), & (a \neq b),
\end{cases} i 1 = 0 ∑ m ⋯ i n = 0 ∑ m i a i b = { 3 1 m n + 2 + o ( m n + 2 ) , 4 1 m n + 2 + o ( m n + 2 ) , ( a = b ) , ( a = b ) ,
我们有
S x 1 + S x 2 + ⋯ + S x n = ( n 2 4 + n 12 ) m n + 2 + o ( m n + 2 ) , S y = ( σ 2 n 2 2 − σ n 2 2 + n 2 8 + n 24 ) m n + 2 + o ( m n + 2 ) , S z = ( σ 2 n 2 2 ) m n + 2 + o ( m n + 2 ) , S e 1 + S e 2 + ⋯ + S e n = ( n 2 4 + n 12 ) m n + 2 + o ( m n + 2 ) \begin{aligned}
S_{x_1} + S_{x_2} + \cdots + S_{x_n} &=(\frac{n^2} {4} + \frac{n}{12})m^{n+2} + o(m^{n+2}),\\
S_y &= (\frac{\sigma^2 n^2} {2} - \frac{\sigma n^2} {2} + \frac{n^2}{8} + \frac{n}{24})m^{n+2} + o(m^{n+2}),\\
S_z &= (\frac{\sigma^2 n^2 }{2})m^{n+2} + o(m^{n+2}),\\
S_{e_1} + S_{e_2} + \cdots + S_{e_n}&= (\frac{n^2 }{4} + \frac{n}{12})m^{n+2} + o(m^{n+2})
\end{aligned} S x 1 + S x 2 + ⋯ + S x n S y S z S e 1 + S e 2 + ⋯ + S e n = ( 4 n 2 + 1 2 n ) m n + 2 + o ( m n + 2 ) , = ( 2 σ 2 n 2 − 2 σ n 2 + 8 n 2 + 2 4 n ) m n + 2 + o ( m n + 2 ) , = ( 2 σ 2 n 2 ) m n + 2 + o ( m n + 2 ) , = ( 4 n 2 + 1 2 n ) m n + 2 + o ( m n + 2 )
其中 s = σ n m s = \sigma nm s = σ n m 0 ≤ σ < 1 0 \leq \sigma < 1 0 ≤ σ < 1
另一方面,维数为
dim ( L ′ ) = ∑ i 1 = 0 m ⋯ ∑ i n = 0 m ∑ k = 0 i 1 + ⋯ + i n ∑ j 1 = 0 m − i 1 ⋯ ∑ j n = 0 m − i n 1 = n 6 ⋅ 2 n − 1 m 2 n + 1 + o ( m 2 n + 1 ) \text{dim}({\mathcal{L}}') = \sum_{i_1=0}^{m} \cdots \sum_{i_n=0}^{m} \sum_{k=0}^{i_1 + \cdots + i_n} \sum_{j_1=0}^{m-i_1} \cdots \sum_{j_n=0}^{m-i_n} 1 = \frac{n}{6 \cdot 2^{n-1}} m^{2n+1} + o(m^{2n+1})
dim ( L ′ ) = i 1 = 0 ∑ m ⋯ i n = 0 ∑ m k = 0 ∑ i 1 + ⋯ + i n j 1 = 0 ∑ m − i 1 ⋯ j n = 0 ∑ m − i n 1 = 6 ⋅ 2 n − 1 n m 2 n + 1 + o ( m 2 n + 1 )
计算细节请参考附录。
通过引用引理1和引理2,我们可以得到整数方程,当
\begin{equation}
\det({\mathcal{L}}') ^ \frac{1}{\text{dim}({\mathcal{L}}')} < (e_1\cdots e_n)^m
\end{equation}
忽略m m m X l = N 1 + 2 δ X_l = N^{1+2\delta} X l = N 1 + 2 δ Y = N 1 2 Y = N^{\frac{1}{2}} Y = N 2 1 Z = N 1 2 Z = N^{\frac{1}{2}} Z = N 2 1 e l ≃ N {e_l} \simeq N e l ≃ N l = 1 , … , n l = 1, \ldots , n l = 1 , … , n
( 1 + δ ) ( n 2 4 + n 12 ) + 1 2 ( σ 2 n 2 2 − σ n 2 2 + n 2 8 + n 24 ) + 1 2 ( σ 2 n 2 2 ) + ( n 2 4 + n 12 ) ≤ n 2 2 (1 + \delta)\left(\frac{n^2}{4} + \frac{n}{12}\right) +
\frac{1}{2}\left(\frac{\sigma^2n^2}{2} - \frac{\sigma n^2}{2}+\frac{n^2}{8}+\frac{n}{24}\right) +
\frac{1}{2}(\frac{\sigma^2 n^2 }{2}) + (\frac{n^2 }{4} + \frac{n}{12}) \leq \frac{n^2 }{2}
( 1 + δ ) ( 4 n 2 + 1 2 n ) + 2 1 ( 2 σ 2 n 2 − 2 σ n 2 + 8 n 2 + 2 4 n ) + 2 1 ( 2 σ 2 n 2 ) + ( 4 n 2 + 1 2 n ) ≤ 2 n 2
通过选择 δ = 1 4 \delta=\frac{1}{4} δ = 4 1 δ \delta δ
δ < 9 n − 14 24 n + 8 \delta < \frac{9n - 14}{24n + 8}
δ < 2 4 n + 8 9 n − 1 4
然后在假设 1 下,可以在多项式时间内对 N N N
我们的结果优于文献中先前的工作的原因基于以下两点观察。首先,我们可以利用 Minkowski 和格构造将 n n n N = p q N = pq N = p q z s z^s z s z z z q q q s s s
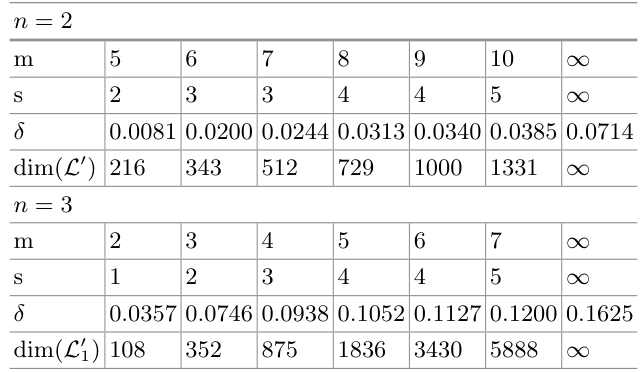
实验结果 。需要注意的是,在定理2的计算中,我们假设 m m m m m m m m m n n n δ \delta δ m m m n n n δ \delta δ
m m m δ \delta δ
我们在一台配备 Intel® Core™ Duo CPU(2.53 GHz,1.9 GB RAM, Windows 7)的个人电脑上,使用 Magma 2.11计算机代数系统[3]实现了实验程序,并进行了 L 3 L^3 L 3
在实验中,我们成功地在实践中分解了共同模 N N N N 0.035 N^{0.035} N 0 . 0 3 5 N N N N 0.015 N^{0.015} N 0 . 0 1 5 N 0.029 N^{0.029} N 0 . 0 2 9
需要注意的是,在实验中,我们总是找到许多多项式方程在整数域上共享所需的解。此外,我们还有另一个方程 y z = N yz = N y z = N
在我们进行的所有验证我们提出的攻击的实验中,我们确实通过使用 Gröbner 基础技术成功地收集了根,并且没有实验结果与假设1相矛盾。然而,另一方面,证明或证实其有效性似乎非常困难。
定理3 . 设 ( e 1 , e 2 , … , e n ) (e_1, e_2, \ldots , e_n) ( e 1 , e 2 , … , e n ) n n n N = p r q N=p^rq N = p r q d 1 , d 2 , ⋯ , d n d_1, d_2, \cdots , d_n d 1 , d 2 , ⋯ , d n
δ < ( r − 1 ) ( r + 1 ) n + 1 n \delta < \frac{(r - 1)}{(r + 1)} ^ \frac{n+1}{n}
δ < ( r + 1 ) ( r − 1 ) n n + 1
时,可以在多项式时间内分解 N N N d l ≤ N δ d_l \leq N^\delta d l ≤ N δ l = 1 , … , n l = 1, \ldots , n l = 1 , … , n
证明. 对于一个模 N = p r q N=p^rq N = p r q n n n ( e l , d l ) (e_l, d_l) ( e l , d l )
e 1 d 1 = k 1 p r − 1 ( p − 1 ) ( q − 1 ) + 1 , e 2 d 2 = k 2 p r − 1 ( p − 1 ) ( q − 1 ) + 1 , ⋯ e n d n = k n p r − 1 ( p − 1 ) ( q − 1 ) + 1 , \begin{aligned}
&e_1 d_1 = k_1 p^{r-1} (p - 1)(q - 1) + 1,\\
&e_2 d_2 = k_2 p^{r-1} (p - 1)(q - 1) + 1,\\
&\cdots\\
&e_n d_n = k_n p^{r-1} (p - 1)(q - 1) + 1,\\
\end{aligned} e 1 d 1 = k 1 p r − 1 ( p − 1 ) ( q − 1 ) + 1 , e 2 d 2 = k 2 p r − 1 ( p − 1 ) ( q − 1 ) + 1 , ⋯ e n d n = k n p r − 1 ( p − 1 ) ( q − 1 ) + 1 ,
因此,对于未知的 ( d 1 , ⋯ , d n ) (d_1, \cdots , d_n) ( d 1 , ⋯ , d n )
e 1 d 1 = k 1 p r − 1 ( p − 1 ) ( q − 1 ) + 1 , e 2 d 2 = k 2 p r − 1 ( p − 1 ) ( q − 1 ) + 1 , ⋯ e n d n = k n p r − 1 ( p − 1 ) ( q − 1 ) + 1 , \begin{aligned}
&e_1 d_1 = k_1 p^{r-1} (p - 1)(q - 1) + 1,\\
&e_2 d_2 = k_2 p^{r-1} (p - 1)(q - 1) + 1,\\
&\cdots\\
&e_n d_n = k_n p^{r-1} (p - 1)(q - 1) + 1,\\
\end{aligned} e 1 d 1 = k 1 p r − 1 ( p − 1 ) ( q − 1 ) + 1 , e 2 d 2 = k 2 p r − 1 ( p − 1 ) ( q − 1 ) + 1 , ⋯ e n d n = k n p r − 1 ( p − 1 ) ( q − 1 ) + 1 ,
正如所示,( d 1 , d 2 , ⋯ , d n ) (d_1, d_2, \cdots , d_n) ( d 1 , d 2 , ⋯ , d n ) d l ≤ N δ d_l \leq N^\delta d l ≤ N δ l = 1 , … , n l = 1, \ldots , n l = 1 , … , n
利用[4,22]中的技术,可以证明如果
δ < ( r − 1 ) ( r + 1 ) ( n + 1 ) n \delta <
\frac{(r - 1)}{(r + 1)} ^ \frac{(n+1)}{n} δ < ( r + 1 ) ( r − 1 ) n ( n + 1 )
在假设1下,这些联立模线性方程可以被解,这意味着 ( d 1 , ⋯ , d n ) (d_1, \cdots , d_n) ( d 1 , ⋯ , d n ) N N N
实验结果 . 我们在 Magma 2.11中实现了实验程序。在所有实验中,我们成功地求解了所需的解 ( d 1 , d 2 , ⋯ , d n ) (d_1, d_2, \cdots , d_n) ( d 1 , d 2 , ⋯ , d n )
N N N
需要注意的是,前述的定理3可以适用于任意大小的加密指数 ( e 1 , ⋯ , e n ) (e_1, \cdots , e_n) ( e 1 , ⋯ , e n ) ( e 1 , d 1 ) (e_1, d_1) ( e 1 , d 1 ) ( e 2 , d 2 ) (e_2, d_2) ( e 2 , d 2 ) e 1 e_1 e 1 e 2 e_2 e 2 N N N N α N^α N α d 1 ≃ d 2 ≃ N δ d_1 \simeq d_2 \simeq N^\delta d 1 ≃ d 2 ≃ N δ
给定两个方程 e 1 d 1 = k 1 p r − 1 ( p − 1 ) ( q − 1 ) + 1 e_1d_1 = k_1p^{r-1}(p - 1)(q - 1) + 1 e 1 d 1 = k 1 p r − 1 ( p − 1 ) ( q − 1 ) + 1 e 2 d 2 = k 2 p r − 1 ( p − 1 ) ( q − 1 ) + 1 e_2d_2 = k_2p^{r-1}(p - 1)(q - 1) + 1 e 2 d 2 = k 2 p r − 1 ( p − 1 ) ( q − 1 ) + 1 p r − 1 ( p − 1 ) ( q − 1 ) p^{r-1}(p - 1)(q - 1) p r − 1 ( p − 1 ) ( q − 1 )
k 2 ( e 1 d 1 − 1 ) = k 1 ( e 2 d 2 − 1 ) k_2(e_1d_1 - 1) = k_1(e_2d_2 - 1)
k 2 ( e 1 d 1 − 1 ) = k 1 ( e 2 d 2 − 1 )
这启示我们寻找多项式
\begin{equation}
f(x, y) = e_2x + y (mod e_1)
\end{equation}
的小解。
由于 ( d 2 k 1 , k 2 − k 1 ) (d_2k_1, k_2-k_1) ( d 2 k 1 , k 2 − k 1 ) f ( x , y ) ( m o d e 1 ) f(x, y) \pmod {e_1} f ( x , y ) ( m o d e 1 ) k 1 k_1 k 1 N α + δ − 1 N^{α+\delta-1} N α + δ − 1 ∣ d 2 k 1 ∣ ≃ X = N α + 2 δ − 1 |d_2k_1| \simeq X = N^{α+2\delta-1} ∣ d 2 k 1 ∣ ≃ X = N α + 2 δ − 1 ∣ k 2 − k 1 ∣ ≃ Y = N α + δ − 1 |k_2 - k_1| \simeq Y = N^{α+\delta-1} ∣ k 2 − k 1 ∣ ≃ Y = N α + δ − 1 X Y < e XY < e X Y < e α + 2 δ − 1 + α + δ − 1 < α α + 2\delta - 1 + α + \delta - 1 < α α + 2 δ − 1 + α + δ − 1 < α ( d 2 k 1 , k 2 − k 1 ) (d_2k_1, k_2 - k_1) ( d 2 k 1 , k 2 − k 1 )
因此,要从这个基于格的方法中恢复 d 2 k 1 d_2k_1 d 2 k 1 k 2 − k 1 k_2 - k_1 k 2 − k 1
α + 3 δ < 2 α + 3\delta < 2
α + 3 δ < 2
其中 α + δ > 1 α + \delta > 1 α + δ > 1
在本文中,我们提出了基于 Minkowski 和的格构造的一些应用,并对多对 CRT-RSA 模数 N N N d p i , d q i ≤ N 2 l − 3 8 l + 2 d_{p_{i}},d_{q_{i}}\le N^{\frac{2l-3}{8l+2}} d p i , d q i ≤ N 8 l + 2 2 l − 3 d p i d_{p_{i}} d p i d q i d_{q_{i}} d q i N 9 l − 14 24 l + 8 N^{\frac{9l-14}{24l+8}} N 2 4 l + 8 9 l − 1 4 N N N i = 1 , 2 , ⋯ , l i = 1, 2, \cdots, l i = 1 , 2 , ⋯ , l N = p r q N = p^rq N = p r q
作者要感谢匿名审稿人对本文的有益评论和建议。本文的工作得到了中国国家重点基础研究计划(项目编号2013CB834203和2011CB302400)、中国国家自然科学基金(项目编号61472417、61402469、61472416和61272478)、中国科学院战略性先导科技专项(项目编号 XDA06010702和 XDA06010703)以及中国科学院信息安全国家重点实验室的支持。Y. Lu 受到 JST 项目 CREST 的支持。
这里给出计算 S X 1 , S Y , S Z 1 , S e 1 S_{X_{1}},S_{Y},S_{Z_{1}},S_{e_{1}} S X 1 , S Y , S Z 1 , S e 1
设对于任意 0 ≤ a , b ≤ n 0\leq a,b\leq n 0 ≤ a , b ≤ n ∑ ∗ \sum^{*} ∑ ∗ ∑ i 1 = 0 m ⋯ ∑ i n = 0 m ∑ j ˙ 1 = 0 m − i 1 ⋯ ∑ j n = 0 m − i n \sum_{i_{1}=0}^{m}\dots \sum_{i_{n}=0}^{m}\sum_{\dot j_1=0}^{m-i_1}\dots\sum_{j_n=0}^{m-i_n} ∑ i 1 = 0 m ⋯ ∑ i n = 0 m ∑ j ˙ 1 = 0 m − i 1 ⋯ ∑ j n = 0 m − i n
∑ ∗ i a i b = { 1 12 ∗ 2 n − 1 ∗ m 2 n + 2 + o ( m 2 n + 2 ) , ( a = b ) , 1 18 ∗ 2 n − 1 ∗ m 2 n + 2 + o ( m 2 n + 2 ) , ( a ≠ b ) , \stackrel{*}{\sum}i_{a}i_{b}=\left\{
\begin{array}{l}
{\frac{1}{12*2^{n-1}}*m^{2n+2}+o(m^{2n+2}),\;(a=b),}\\
{\frac{1}{18*2^{n-1}}*m^{2n+2}+o(m^{2n+2}),\;(a\neq b),}
\end{array}\right. ∑ ∗ i a i b = { 1 2 ∗ 2 n − 1 1 ∗ m 2 n + 2 + o ( m 2 n + 2 ) , ( a = b ) , 1 8 ∗ 2 n − 1 1 ∗ m 2 n + 2 + o ( m 2 n + 2 ) , ( a = b ) ,
和
∑ ⋆ i a j b = { 1 24 ∗ 2 n − 1 ∗ m 2 n + 2 + o ( m 2 n + 2 ) , ( a = b ) , 1 18 ∗ 2 n − 1 ∗ m 2 n + 2 + o ( m 2 n + 2 ) , ( a ≠ b ) . \stackrel{\star}{\sum}i_{a}j_{b}=\left
\{\begin{array}{l}
{\frac{1}{24*2^{n-1}}\ast m^{2n+2}+o(m^{2n+2}),\;(a=b),}\\
{\frac{1}{18*2^{n-1}}\ast m^{2n+2}+o(m^{2n+2}),\;(a\neq b).}
\end{array}\right. ∑ ⋆ i a j b = { 2 4 ∗ 2 n − 1 1 ∗ m 2 n + 2 + o ( m 2 n + 2 ) , ( a = b ) , 1 8 ∗ 2 n − 1 1 ∗ m 2 n + 2 + o ( m 2 n + 2 ) , ( a = b ) .
然后我们得到
∑ ∗ ∑ k = 0 i 1 + ⋯ + i n i 1 + ⋯ + i n = ( n 2 18 + n 36 ) ∗ m 2 n + 2 2 n − 1 + o ( m 2 n + 2 ) , ∑ ∗ ∑ k = 0 i 1 + ⋯ + i n j 1 + ⋯ + j n = ( n 2 18 − n 72 ) ∗ m 2 n + 2 2 n − 1 + o ( m 2 n + 2 ) , ∑ ∗ ∑ k = 0 i 1 + ⋯ + i n k = ∑ ∗ ( i 1 + ⋯ + i n ) 2 2 + i 1 + ⋯ + i n 2 = ( n 2 36 + n 72 ) ∗ m 2 n + 2 2 n − 1 + o ( m 2 n + 2 ) . \begin{aligned}
\sum^{*}\sum_{k=0}^{i_{1}+\cdots+i_{n}}i_{1}+\cdots+i_{n}&=({\frac{n^{2}}{18}}+{\frac{n}{36}})*{\frac{m^{2n+2}}{2^{n-1}}}+o(m^{2n+2}),\\
\sum^{*}\sum_{k=0}^{i_{1}+\dots+i_{n}}j_{1}+\dots+j_{n}&=({\frac{n^{2}}{18}}-{\frac{n}{72}})*{\frac{m^{2n+2}}{2^{n-1}}}+o(m^{2n+2}),\\
\sum^{*}\sum_{k=0}^{i_{1}+\cdots+i_{n}}k&=\sum_{\,}^{*}\frac{(i_{1}+\cdots+i_{n})^{2}}{2}+\frac{i_{1}+\cdots+i_{n}}{2}\\
&=\left(\frac{n^{2}}{36}+\frac{n}{72}\right)*\frac{m^{2n+2}}{2n-1}+o(m^{2n+2}).
\end{aligned} ∑ ∗ k = 0 ∑ i 1 + ⋯ + i n i 1 + ⋯ + i n ∑ ∗ k = 0 ∑ i 1 + ⋯ + i n j 1 + ⋯ + j n ∑ ∗ k = 0 ∑ i 1 + ⋯ + i n k = ( 1 8 n 2 + 3 6 n ) ∗ 2 n − 1 m 2 n + 2 + o ( m 2 n + 2 ) , = ( 1 8 n 2 − 7 2 n ) ∗ 2 n − 1 m 2 n + 2 + o ( m 2 n + 2 ) , = ∑ ∗ 2 ( i 1 + ⋯ + i n ) 2 + 2 i 1 + ⋯ + i n = ( 3 6 n 2 + 7 2 n ) ∗ 2 n − 1 m 2 n + 2 + o ( m 2 n + 2 ) .
此外,
∑ ∗ ∑ k = 0 i 1 + ⋯ + i n min ( i 1 , k ) = ∑ ∗ ( ∑ k = 0 i 1 k + ∑ k = i 1 + 1 i 1 + ⋯ + i n i 1 ) = ∑ ∗ ( i 1 ( i 1 + 1 ) 2 + i 1 ( i 2 + ⋯ + i n ) ) = ( n 18 − 1 72 ) ∗ m 2 n + 2 2 n − 1 + o ( m 2 n + 2 ) \begin{aligned}
\sum^*\sum_{k=0}^{i_{1}+\cdots+i_{n}}\min(i_{1},k)&=\sum^*(\sum^{i_1}_{k=0}k+\sum_{k=i_1+1}^{i_{1}+\cdots+i_{n}}i_1)\\
&=\sum^*(\frac{i_1(i_1+1)}{2}+i_1(i_2+\cdots + i_n))\\
&=(\frac{n}{18}-\frac{1}{72})*\frac{m^{2n+2}}{2^{n-1}}+o(m^{2n+2})\\
\end{aligned} ∑ ∗ k = 0 ∑ i 1 + ⋯ + i n min ( i 1 , k ) = ∑ ∗ ( k = 0 ∑ i 1 k + k = i 1 + 1 ∑ i 1 + ⋯ + i n i 1 ) = ∑ ∗ ( 2 i 1 ( i 1 + 1 ) + i 1 ( i 2 + ⋯ + i n ) ) = ( 1 8 n − 7 2 1 ) ∗ 2 n − 1 m 2 n + 2 + o ( m 2 n + 2 )
通过对称,我们有
∑ ∗ ∑ k = 0 i 1 + ⋯ + i n ∗ m i n ( i 1 , k ) + ⋅ ⋅ ⋅ + ∗ m i n ( i n , k ) = ( n 2 18 − n 72 ) ∗ m 2 n + 2 2 n − 1 + o ( m 2 n + 2 ) . \sum^{\ast}\sum_{k=0}^{i_{1}+\dots+i_{n}}{*{min}}(i_{1},k)+\cdot\cdot\cdot+*{min}(i_{n},k)=(\frac{n^{2}}{18}-\frac{n}{72})\ast\frac{m^{2n+2}}{2^{n-1}}+o(m^{2n+2}).
∑ ∗ k = 0 ∑ i 1 + ⋯ + i n ∗ m i n ( i 1 , k ) + ⋅ ⋅ ⋅ + ∗ m i n ( i n , k ) = ( 1 8 n 2 − 7 2 n ) ∗ 2 n − 1 m 2 n + 2 + o ( m 2 n + 2 ) .
格 L ′ {\mathcal{L}}^{\prime} L ′
d i m ( L ′ ) = ∑ ∗ ∑ k = 0 i 1 + ⋯ + i n 1 = n 6 ∗ 2 n − 1 ∗ m 2 n + 1 + o ( m 2 n + 1 ) . \mathrm{dim}({\mathcal L}^{\prime})=\sum^{*}\sum_{k=0}^{i_{1}+\dots+i_{n}}1=\frac n{6*2^{n-1}}*m^{2n+1}+o(m^{2n+1}).
d i m ( L ′ ) = ∑ ∗ k = 0 ∑ i 1 + ⋯ + i n 1 = 6 ∗ 2 n − 1 n ∗ m 2 n + 1 + o ( m 2 n + 1 ) .