GAMES101-6(1):反走样
前言
GAMES101-P6:反走样
走样现象
瑕疵(Artifact):图形学中的一切错误、误差、不准确等。
经过采样以后,会看到明显的锯齿边缘,这是一种走样现象。
常见的走样现象:锯齿、摩尔纹、频闪效应
走样不仅可以发生在空间中,时间上也可以走样。例如频闪效应。
采样现象产生的原因:信号变化的频率对于采样频率而言高。(奈奎斯特定理)
采样频率高于信号频率两倍,才能完全恢复信息。
傅里叶变换
傅里叶变换:任何函数可以可以用一系列的基本三角函数的组合表示。
通过傅里叶变换我们可以将图像由时域迁移到频域。并且可以发现,对于大部分正常的图像,大部分信息集中在低频,高频信息很少。
我们应用滤波:
- 高通滤波:我们忽略掉低频信息,只保留高频信息,那么就能得到图像的边界(像素迅速变化的地方)。
- 低通滤波:我们忽略掉高频信息,只保留低频信息。那么就能得到模糊的图像。
- 保留区间内频率:一些不太明显的边界(太明显的当然是非常高频的信息)。
我们可以认为:滤波=卷积=平均(卷积的概念见维基)
卷积定理:时域上两个信号的卷积等价于频域上它们信号的乘积。
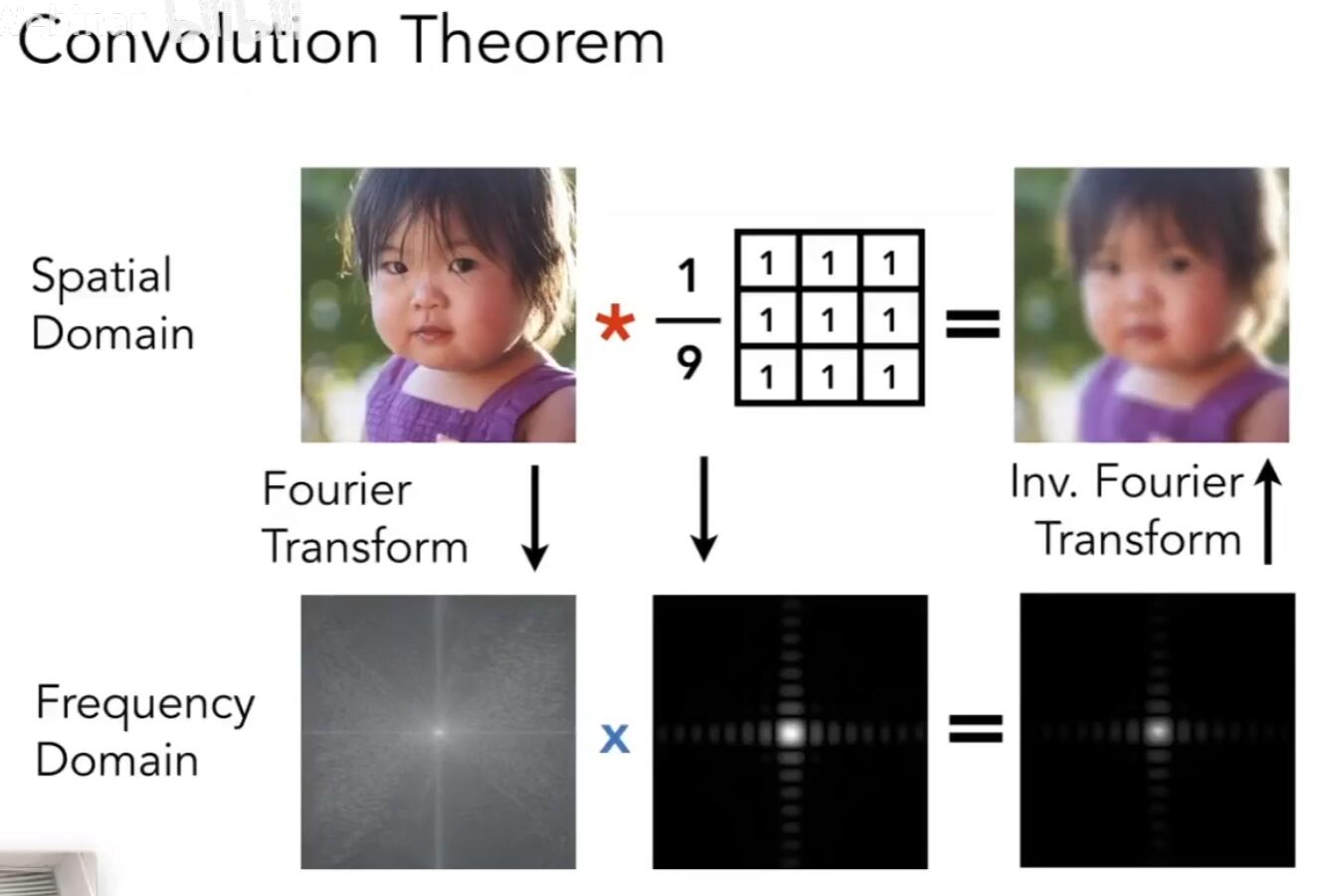
越大的卷积盒会保留越低的频率,带来越模糊的图像。
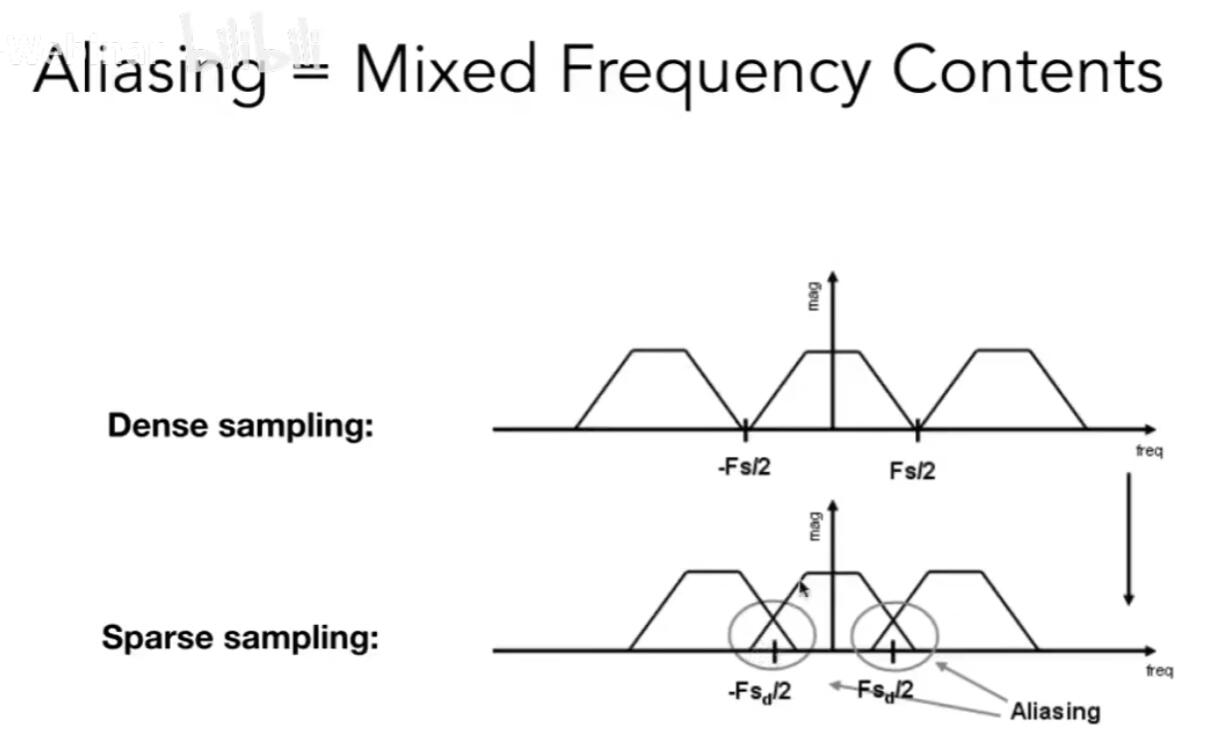
从频谱的角度理解采样:
- 采样就是在不同的频域上复制原有的频谱
- 采样率不够高,那么不同频域上的频谱就会混叠在一起
反走样的办法
-
增加采样率:简单暴力,直接提高采样率。
-
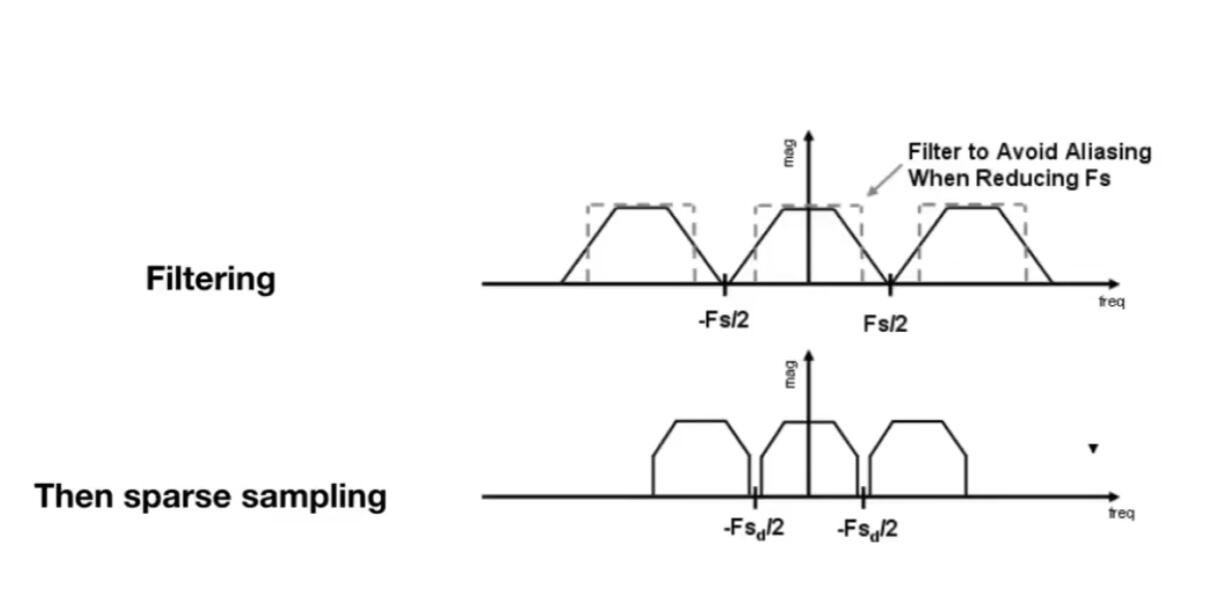
Pre-Filter:预先滤波。首先用滤波对原图进行模糊,这样边缘有的像素就会点上介乎于边界两边的中间色,例如更浅的颜色。
滤波必须在采样之前进行,否则得到的是模糊的锯齿(Blurred aliasing),没有很好的反走样效果。
因为真实边界信息在采样过程中已经损失了,所以滤波只能平均/模糊错误的信息。
从频率的角度来理解,滤波的作用是削去了高频信号,这样就占用的频率带宽变小,原本会混叠的信号就不会混叠了
-
MSAA:对一个像素内设置更多的采样点。例如四个角各有一个像素点,如果只有 x 个点被覆盖就是 x/4 的灰度。
MSAA 并没有提高分辨率,只是提高了一个像素内的采样数量。
当然,MSAA 会显著提高计算量,不过当代工业界会通过复用像素等方法来降低消耗。4x MSAA 并不会让游戏帧率降低到 1/4。
-
FXAA(Fast Approxim AA):不对图像而对图片进行处理。得到图像以后,图像匹配找到有锯齿的边界,用没有锯齿的边界进行替换。
-
TAA:复用上一帧的结果。
跳转
Home:GAMES101-1:课程总览与笔记导航
Prev:GAMES101-5:(三角形的)光栅化